【题目】阅读下列材料,并解答其后的问题:
我国古代南宋数学家秦九韶在其所著书《数学九章》中,利用“三斜求积术”十分巧妙的解决了已知三角形三边求其面积的问题,这与西方著名的“海伦公式”是完全等价的.我们也称这个公式为“海伦秦九韶公式”,该公式是:设△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,△ABC的面积为S=![]() .
.
(1)(举例应用)已知△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a=4,b=5,c=7,则△ABC的面积为 ;
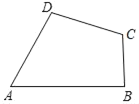
(2)(实际应用)有一块四边形的草地如图所示,现测得AB=(2![]() +4
+4![]() )m,BC=5m,CD=7m,AD=4
)m,BC=5m,CD=7m,AD=4![]() m,∠A=60°,求该块草地的面积.
m,∠A=60°,求该块草地的面积.
参考答案:
【答案】(1)![]() (2)(12
(2)(12![]() +24+5
+24+5![]() )m2
)m2
【解析】
(1)由已知△ABC的三边a=4,b=5,c=7,可知这是一个一般的三角形,故选用海伦-奏九韶公式求解即可;(2)过点D作DE⊥AB,垂足为E,连接BD.将所求四边形的面积转化为三个三角形的面积的和进行计算。
(1)解:△ABC的面积为S=![]() =
=![]() =4
=4![]()
故答案是:4![]() ;
;
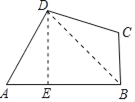
(2)解:如图:过点D作DE⊥AB,垂足为E,连接BD(如图所示)
在Rt△ADE中,
∵∠A=60°,
∴∠ADE=30°,
∴AE=![]() AD=2
AD=2![]()
∴BE=AB﹣AE=2![]() +4
+4![]() ﹣2
﹣2![]() =4
=4![]()
DE=![]()
∴BD=![]()
∴S△BCD=![]()
∵S△ABD=![]()
∴S四边形ABCD=S△BCD+S△ABD= ![]()
答:该块草地的面积为(![]() )m2.
)m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
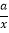 (a>0,a为常数)和y=
(a>0,a为常数)和y= 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=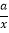 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y= 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y= 的图象于点B.当点M在y=
的图象于点B.当点M在y=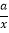 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的个数是( )
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的个数是( ) 
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上有A、B、C三个点,它们表示的数分别是-24,-10,10.A、B两点间的距离记为“AB”.

(1)填空:AB= ,BC= ;
(2)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位 长度和7个单位长度的速度向右运动,设运动时间为t,用含t的代数式表示BC和AB的长,试探索:BC - AB的值是否随着时间t的变化而改变?请说明理由.
(3)现有动点P、Q都从A点出发,点P以每秒1个单位长度的速度向终点C移动;当点P 移动到B点时,点Q才从A点出发,并以每秒3个单位长度的速度向右移动,且当点P到达C点时,点Q就停止移动.设点P移动的时间为t秒,问:当t为多少时P、Q两点相距6个单位长度?
-
科目: 来源: 题型:
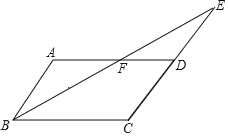
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF,
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A、O、E三点在同一条直线上,∠AOB=∠COD=90°,观察图形后有以下四个结论,其中正确的结论是( )
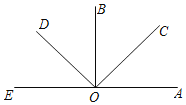
A.∠BOC=∠AOC=∠BOD
B.图中小于平角的角有6个
C.∠BOC与∠AOD互补
D.∠BOD和∠AOC互余
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏为了解本市的空气质量情况,从市环保局随机抽取了若干天的空气质量情况作为标本进行统计,绘制成如图所示的条形统计图和扇形统计图(部分信息为给出)
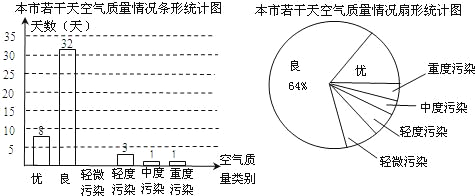
请你根据图中提供的信息,解答下列问题:
(1)本次调查中共抽取了多少天的空气质量情况作为标本?
(2)求轻微污染天数并补全条形统计图;
(3)请你估计该市这一年(365天)空气质量达到“优”和“良”的总天数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

