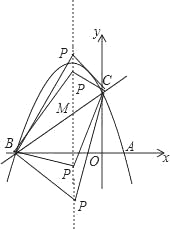
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.

参考答案:
【答案】(1)抛物线解析式为y=﹣x2﹣2x+3,直线BC的解析式为y=x+3;
(2)即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);
(3)P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1,![]() ) 或(﹣1,
) 或(﹣1,![]() ).
).
【解析】试题分析:(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
试题解析:(1)依题意得: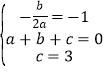 ,
,
解之得: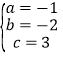
∴抛物线解析式为y=-x2-2x+3
∵对称轴为x=-1,且抛物线经过A(1,0),
∴把B(-3,0)、C(0,3)分别代入直线y=mx+n,
得![]() ,
,
解之得:![]() ,
,
∴直线y=mx+n的解析式为y=x+3;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得,y=2,
∴M(-1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2);
(3)设P(-1,t),
又∵B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,
PC2=(-1)2+(t-3)2=t2-6t+10,
①若点B为直角顶点,则BC2+PB2=PC2
即:18+4+t2=t2-6t+10解之得:t=-2;
②若点C为直角顶点,则BC2+PC2=PB2
即:18+t2-6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2
即:4+t2+t2-6t+10=18解之得:t1=![]() ,t2=
,t2=![]() ;
;
综上所述P的坐标为(-1,-2)或(-1,4)或(-1,![]() ) 或(-1,
) 或(-1,![]() ).
).
-
科目: 来源: 题型:
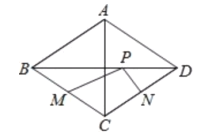
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A.
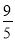 B.3
B.3C.
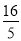 D.5
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|=6+7;|6-7|=7-6;|7-6|=7-6;|-6-7|=6+7;
根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=_________;
(2)|-
 +0.8|=____________;
+0.8|=____________;(3)|
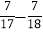 |=__________;
|=__________;(4)用合理的方法计算:|
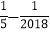 |+|
|+|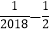 |-|-
|-|- |-
|- ×|-
×|- |+
|+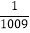 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当∠BAC= 时,矩形AEBD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序如下:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试.两个程序的结果统计如下:

测试项目
测试成绩/分
甲
乙
丙
笔试
92
90
95
面试
85
95
80
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,已知AD//BC,∠ABC=90°.

(1)若AC⊥BD,且AC=5,BD=3(如图1),求四边形ABCD的面积;
(2)若DE⊥BC于E,F是CD的中点,BD=BC,(如图2),求证:∠BAF=∠BCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果
乙种糖果
丙种糖果
单价(元/千克)
15
25
30
千克数
40
40
20
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
相关试题

