【题目】把抛物线y=-x2+2的图象绕原点旋转180°,所得的抛物线的函数关系是( )
A. y=x2+2B. y=-x2+2C. y=-x2-2D. y=x2-2
参考答案:
【答案】D
【解析】
根据二次函数y=-x2+2的图象绕原点旋转180°后得到的抛物线顶点坐标不变,只是开口方向相反求解即可.
抛物线y=-x2+2的顶点坐标为(0,2),
因为二次函数y=-x2+2的图象绕原点旋转180°后得到的抛物线顶点坐标不变,只是开口方向相反,
所以旋转后的抛物线解析式为y=x2-2.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AD⊥BC于D,EF⊥BC于F,∠3=∠E,求证:AD平分∠BAC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=(x-3)2图像上的两个不同的点A(3,a)和B(x,b),则a和b的大小关系( )
A. a≤bB. a>bC. a<bD. a≥b
-
科目: 来源: 题型:
查看答案和解析>>【题目】
乐天借到一本有72页的图书,要在10天之内读完,开始两天每天只读5页,那么以后几天里每天至少要读多少页?设以后几天里每天要读x页,所列不等式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD垂足为M,EN⊥CD垂足为N.
(1)当AD=CD时,求证:DE∥AC;
(2)探究:AD为何值时,△BME与△CNE相似?
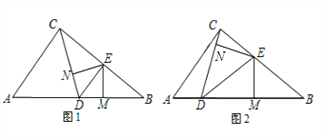
-
科目: 来源: 题型:
查看答案和解析>>【题目】个不透明的口袋里装有分别标有汉字“美”、“丽”、“西”、“湖”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“西”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用画树状图的方法,求出甲取出的两个球上的汉字恰能组成“美丽”或“西湖”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,再从中任取一球,记乙取出的两个球上的汉字恰能组成“美丽”或“西湖”的概率为P2,请比较P1,P2的大小关系。
-
科目: 来源: 题型:
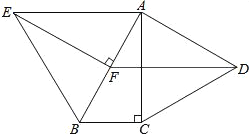
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
相关试题

