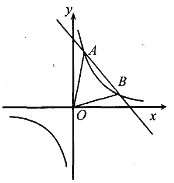
【题目】如图所示,在直角坐标系 xOy 中,一次函数![]() =
=![]() x+b(
x+b(![]() ≠0)的图象与反比例函数
≠0)的图象与反比例函数 ![]()
![]() 的图象交于A(1,4),B(2,m)两点.
的图象交于A(1,4),B(2,m)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB 的面积;
(3)当 x 的取值范围是 时,![]() x+b>
x+b>![]() (直接将结果填在横线上)
(直接将结果填在横线上)
参考答案:
【答案】(1)![]() ,
,![]() ;(2)3;(3)x<0或
;(2)3;(3)x<0或![]()
【解析】
(1)把(1,4)代入y=![]() ,易求k2,从而可求反比例函数解析式,再把B点坐标代入反比例函数解析式,易求m,然后把A、B两点坐标代入一次函数解析式,易得关于k1、b的二元一次方程,解可求k1、b,从而可求一次函数解析式;
,易求k2,从而可求反比例函数解析式,再把B点坐标代入反比例函数解析式,易求m,然后把A、B两点坐标代入一次函数解析式,易得关于k1、b的二元一次方程,解可求k1、b,从而可求一次函数解析式;
(2)设直线AB与x轴交于点C,再根据一次函数解析式,可求C点坐标,再根据分割法可求△AOB的面积;
(3)观察可知当x<0或1<x<3时,k1x+b>![]() .
.
解:(1)把(1,4)代入y=![]() ,得
,得
k2=4,
∴反比例函数的解析式是y=![]() ,
,
当x=2时,y=![]() ,
,
∴m=2,
把(1,4)、(2,2)代入y1=k1x+b中,得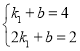 ,
,
解得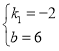 ,
,
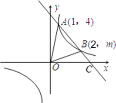
∴一次函数的解析式是y=-2x+6;
(2)设直线AB与x轴交于点C,
当y=0时,x=3,
故C点坐标是(3,0),
∴S△AOB=S△AOC-S△BOC=![]() ×3×4-
×3×4-![]() ×3×2=6-3=3;
×3×2=6-3=3;
(3)在第一象限,当1<x<2时,k1x+b>![]() ;
;
还可观察可知,当x<0时,k1x+b>![]() .
.
∴x<0或1<x<2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户去年承包荒山若干亩,投资7800 元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8 人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)该农户加强果园管理,力争到明年纯收入达到15000元,那么纯收入增长率是多少?(纯收入=总收入﹣总支出,该农户采用了(2)中较好的出售方式出售)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
,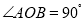 ,
, 平分
平分 .
.
(1)若
 ,则
,则 _______°,
_______°, _______°;
_______°;(2)若
 ,则
,则 ________°,
________°, ________°;
________°;(3)若
 ,
, ,请直接写出
,请直接写出 与
与 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|2a+4|+|b-6|=0

(1)求A,B两点之间的距离;
(2)若在数轴上存在一点C,且AC=2BC,求C点表示的数;
(3)若在原点O处放一个挡板,一个小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动:设运动的时间为(秒).
①分别表示甲、乙两小球到原点的距离(用t表示);
②求甲、乙两小球到原点的距离相等时经历的时间
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P 为△ABC 内一点,连接 PA、PB、PC,在△PAB、△PBC 和△PAC 中,如果存在一个三角形与△ABC 相似,那么就称 P 为△ABC 的自相似点.
(1)如图 2,已知 Rt△ABC 中,∠ACB=90°,CD 是 AB 上的中线,过点 B 作 BE⊥CD,垂足为 E,试说明 E 是△ABC 的自相似点.
(2)如图 3,在△ABC 中,∠A<∠B<∠C.若△ABC 的三个内角平分线的交 点 P 是该 三角形的自相似点,求该三角形三个内角的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C,D在线段AB上,M、N分别是AC、BD的中点,若AB=20,CD=4,
(1)求MN的长.
(2)若AB=a,CD=b,请用含有a、b的代数式表示出MN的长.

-
科目: 来源: 题型:
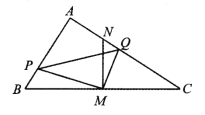
查看答案和解析>>【题目】在△ABC 中,∠BAC=90°,AB<AC,M 是 BC 边的中点,MN⊥BC交 AC 于点 N,动点 P 在线段 BA 上以每秒
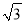 cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).(1)△PBM 与△QNM 相似吗?请说明理由;
(2)若∠ABC=60°,AB=4
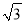 cm.
cm.①求动点 Q 的运动速度;
②设△APQ 的面积为 s(cm2),求 S 与 t 的函数关系式.(不必写出 t 的取值范围)
(3)探求 BP、PQ、CQ 三者之间的数量关系,请说明理由.
相关试题

