【题目】如图,有一直径是![]() 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
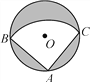
(1)AB的长为多少米?
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面半径为多少米?
参考答案:
【答案】(1)1米(2)![]() 米
米
【解析】
(1)如下图,连接BC,则由已知易得△ABC是等腰直角三角形,且BC=![]() ,∠A=90°,由此可得AB=1;
,∠A=90°,由此可得AB=1;
(2)由AB=1,∠A=90°可得![]() 的长度,而由
的长度,而由![]() 的长度是所围圆锥的底面圆的周长即可计算出底面圆的半径.
的长度是所围圆锥的底面圆的周长即可计算出底面圆的半径.
(1)如下图,连接BC,
∵在☉O中,∠A=90°,
∴BC是☉O的直径,
∴BC=![]() ,
,
又∵AB=AC,
∴AB=1(米);

(2)∵AB=1,∠A=90°,
∴![]() ,
,
设扇形ABC围成的圆锥的底面圆的半径为r,则:
![]() ,解得:
,解得:![]() (米).
(米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(
 ),在四边形
),在四边形 中,
中, ,
, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 .探究图中线段
.探究图中线段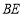 ,
, ,
, 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长 到点
到点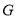 ,使
,使 ,连接
,连接 ,先证明
,先证明 ≌
≌ ,再证明
,再证明 ≌
≌ ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.如图(
 ),若在四边形
),若在四边形 中,
中, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.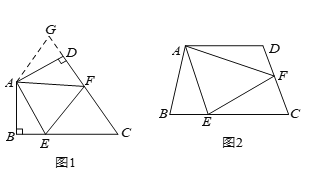
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是_______cm3.

-
科目: 来源: 题型:
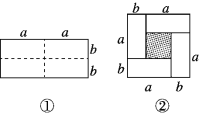
查看答案和解析>>【题目】动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题:
(1)观察图②,请用两种不同的方法表示阴影部分的面积:_____________,_____________;
(2)请写出三个代数式(a+b)2,(a-b)2,ab之间的一个等量关系:___________________________;
问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知x+y=8,xy=7,求x-y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我国某大使馆内有一单杠支架,支架高2.8 m,在大使办公楼前竖立着高28 m的旗杆,旗杆底部离大使办公楼墙根的垂直距离为17 m,在一个阳光灿烂的某一时刻,单杠支架的影长为2.24 m,大使办公室窗口离地面5 m,问此刻中华人民共和国国旗的影子是否能达到大使办公室的窗口?

-
科目: 来源: 题型:
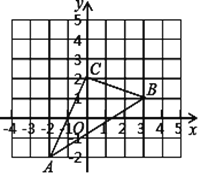
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出
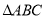 各点的坐标;
各点的坐标;(2)若把△ABC向上平移2个单位,再向左平移1个单位得到
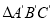 ,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;(3)求出△ABC的面积.
-
科目: 来源: 题型:
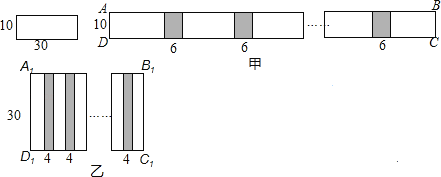
查看答案和解析>>【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).
相关试题

