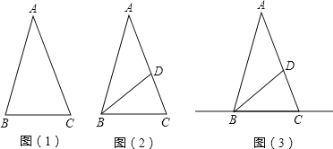
【题目】如图(1),在△ABC中,AB=AC,∠A=36°.
(1)直接写出∠ABC的度数;
(2)如图(2),BD是△ABC中∠ABC的平分线.
①找出图中所有等腰三角形(等腰三角形ABC除外),并选其中一个写出推理过程;
②在直线BC上是否存在点P,使△CDP是以CD为一腰的等腰三角形?如果存在,请在图(3)中画出满足条件的所有的点P,并直接写出相应的∠CPD的度数;如果不存在,请说明理由.
参考答案:
【答案】(1)72°;(2)①△ADB、△BCD是等腰三角形,理由详见解析;②存在3个点P,使得△CDP是等腰三角形,∠CPD的度数详见解析.
【解析】
(1)由已知条件结合等腰三角形的性质及三角形内角和进行求解;
(2)①等腰三角形的判定,BD是△ABC中∠ABC的平分线.可求出各个角的大小再进行判断;
②使△CDP为等腰三角形,则可能是CD=CP,DP=CD,因为∠C=∠BDC,所以不可能PC=PD.
解:(1)∵AB=AC,∠A=36°,∴∠ABC=![]() (180°∠A)==72°;
(180°∠A)==72°;
(2)①如图(2),△ADB、△BCD是等腰三角形.
说明△ADB是等腰三角形,理由:由(1)得:∠ABC=72°,
又∵BD是∠ABC的平分线,∴∠ABD=![]() ∠ABC=36°,
∠ABC=36°,
又∵∠A=36°,∴∠A=∠ABD,
∴AD=BD,即△ADB是等腰三角形;
说明△BCD是等腰三角形,理由:
∵∠A=36°,AB=AC,
∴∠C=∠ABC=![]() (180°-36°)=72°
(180°-36°)=72°
又∵BD是∠ABC的平分线,
∴∠DBC=![]() ∠ABC=36°,
∠ABC=36°,
∴∠BDC=180°-∠C-∠DBC=180°-72°-36°=72°,
∴∠C=∠BDC,
∴BD=BC,即△BCD是等腰三角形;
②存在3个点P,使得△CDP是等腰三角形.如图:
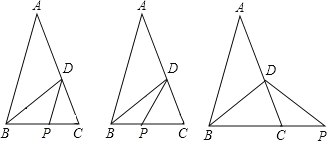
当以∠CDP为顶角,CD为一腰时,∠CPD=72°;
当以∠DCP为顶角,CD为一腰时,存在两点P:
一点在线段BC延长线上,此时∠CPD=36°;
一点在线段BC上,此时∠CPD=54°.
故答案为:(1)72°;(2)①△ADB、△BCD是等腰三角形,理由详见解析;②存在3个点P,使得△CDP是等腰三角形,∠CPD的度数详见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=
 .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
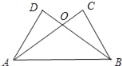
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:△OAB是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90,AC=BC,AD平分∠CAB,DE⊥AB,垂足为E.
(1)求证:CD=BE;
(2)若AB=10,求BD的长度。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB’C’D’,图中阴影部分的面积为( ).

A.
 B.
B.  C.
C. 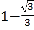 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录的是今年长江某一周内的水位变化情况,这一周的上周末的水位已达到警戒水位
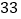 米(正号表示水位比前一天上升,负号表示水位比前一天下降).
米(正号表示水位比前一天上升,负号表示水位比前一天下降). 星期
一
二
三
四
五
六
水位
变化(米)
+0.2
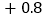
-0.4
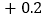
+0.3
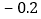
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
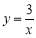 ,
,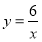 在第一象限内的图象如图所示,点P1,P2,P3,…,P2019在反比例函数
在第一象限内的图象如图所示,点P1,P2,P3,…,P2019在反比例函数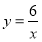 图象上,它们的横坐标分别是x1,x2,x3,…,x2019,纵坐标分别是1,3,5,…,共2019个连续奇数,过点P1,P2,P3,…,P2019分别作y轴的平行线,与
图象上,它们的横坐标分别是x1,x2,x3,…,x2019,纵坐标分别是1,3,5,…,共2019个连续奇数,过点P1,P2,P3,…,P2019分别作y轴的平行线,与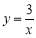 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2019(x2019,y2019),则y2019=________.
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2019(x2019,y2019),则y2019=________. 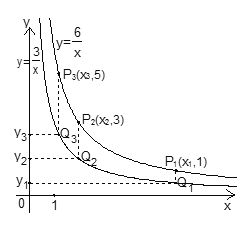
相关试题

