搜索
【题目】解不等式（组）并把解集表示在数轴上
（1）
；（2）
；
（3）
；（4）
参考答案：
【答案】（1） x
；(2 ) x
；(3) 
；(4) 
【解析】分析：（1）根据移项得4x-6x≥-3 -5，移项合并同类项得-2x≥-8，系数化为1即可求得不等式的解集；（2）去分母得2（x+6）-2（9-2x）≤3（5x+1），去括号得2x+12-18+4x≤15x+3，移项合并同类项得-9 x≤-9，系数化为1即可求得不等式的解集；（3）分别求得不等式①②的解集，这两个不等式解集的公共部分即为不等式组的解集；（4）分别求得不等式①②的解集，这两个不等式解集的公共部分即为不等式组的解集．
详解：
（1）4x+5≥6x-3
4x-6x≥-3 -5
-2x≥-8
x≤4；
（2）
2（x+6）-2（9-2x）≤3（5x+1）
2x+12-18+4x≤15x+3
2x+4x-15x≤3+18-12
-9 x≤-9
x；
（3）
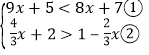
解不等式①得，x<2；
解不等式②得，
；
∴不等式组的解集为：.
（4）
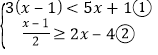
解不等式①得，x>-2；
解不等式②得，
；
∴不等式组的解集为：
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和－1，若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2012次后，点B（ ）
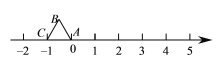
A. 不对应任何数 B. 对应的数是2010 C. 对应的数是2011 D. 对应的数是2012
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将一张等边三角形纸片沿各边中点剪成4个小三角形，称为第一次操作；然后将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；……，根据以上操作，若要得到100个小三角形，则需要操作的次数是( )
A. 25 B. 33 C. 34 D. 50
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索规律，观察下面算式，解答问题．
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+（2n-1）+（2n +1）+(2n +3)=
(3)试计算：101 +103+…+197 +199.
-
科目： 来源： 题型：
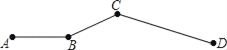
查看答案和解析>>【题目】如图，老王开车从A到D，全程共72千米．其中AB段为平地，车速是30千米/小时，BC段为上山路，车速是22.5千米/小时，CD段为下山路，车速是36千米/小时，已知下山路是上山路的2倍．
（1）若AB=6千米，老王开车从A到D共需多少时间？
（2）当BC的长度在一定范围内变化时，老王开车从A到D所需时间是否会改变？为什么？（给出计算过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，
∠BAD＝45°，AD与BE交于点F，连接CF.
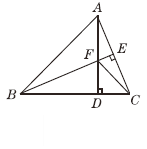
（1）求证：BF＝2AE；
（2）若CD＝
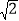，求AD的长. -
科目： 来源： 题型：
查看答案和解析>>【题目】操作探究：已知在纸面上有一数轴(如图所示)．
操作一：
(1)折叠纸面，使1表示的点与－1表示的点重合，则－3表示的点与________表示的点重合；
操作二：
(2)折叠纸面，使－1表示的点与3表示的点重合，回答以下问题：
①5表示的点与数________表示的点重合；
②若数轴上A、B两点之间距离为11(A在B的左侧)，且A、B两点经折叠后重合，求A、B两点表示的数是多少．
相关试题
