【题目】在某一平地上,有一棵树高8米的大树,一棵树高3米的小树,两树之间相距12米。今一只小鸟在其中一棵树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少?(画出草图然后解答)
参考答案:
【答案】小鸟飞的最短距离为13米.
【解析】试题分析:根据题意,先画出示意图,如下图,假设小鸟位于O点上,要飞到B点,根据“两点之间,线段最短”的知识点,可知小鸟沿着OB的方向飞,距离最短.两树之间的距离OA已知,BA为两树高度差,根据勾股定理即可得出OB,即得出小鸟飞的最短距离.
试题解析:
根据题意,画出示意图,如下所示,(画出△ABO即可)
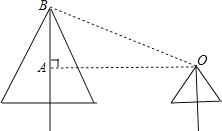
OA=12米,BA=8-3=5米,
根据题意,设小鸟位于O点,
小鸟要飞到B点的最短距离是沿着OB方向飞即可,
根据勾股定理,
OB2=OA2+BA2=169,
即OB=13米.
答:小鸟飞的最短距离为13米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD、BE分别是△ABC的中线,AD、BE相交于点F.
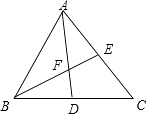
(1)△ABC与△ABD的面积有怎样的数量关系?为什么?
(2)△BDF与△AEF的面积有怎样的数量关系?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题为真命题的是( )
A.直角三角形的两个锐角互余B.任意多边形的内角和为360°
C.任意三角形的外角中最多有一个钝角D.一个三角形中最多有一个锐角
-
科目: 来源: 题型:
查看答案和解析>>【题目】.设m、n为整数,十位数字是m,个位数字是n的两位整数是 ____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x+2=0的根的情况是( )
A.有两个不相等的实数根B.有两个相等的实数根
C.只有一个实数根D.没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】由方程x+5=6得到x=1,依据是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,将三角尺的直角顶点P落在∠AOB的平分线OC的任意一点上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。证明:PE=PF。

相关试题

