【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是△ABC外一点,连接AD、BD、CD,若∠CDB=90°,BD=3,AD= ![]() ,则AC长为 .
,则AC长为 . 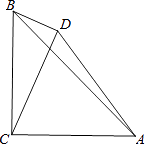
参考答案:
【答案】![]()
【解析】解:作AE⊥CD于E,如图所示: 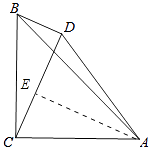
则∠AEC=∠AED=90°,
∴∠ACE+∠CAE=90°,
∵∠ACB=90°,
∴∠BCD=∠CAE,
在△ACE和△CBD中, 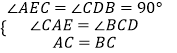 ,
,
∴△ACE≌△CBD(AAS),
∴CE=BD=3,AE=CD,
设AE=x,则DE=x﹣3,
在Rt△ADE中,AE2+DE2=AD2 ,
即x2+(x﹣3)2=( ![]() )2 ,
)2 ,
解得:x=7,或x=﹣4(舍去),
∴AE=7,
在Rt△ACE中,AC= ![]() =
= ![]() =
= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列代数式.
(1)设某数为x,用代数式表示比某数的2倍少1的数;
(2)a,b两数的平方和减去它们的积的2倍;
(3)某工厂第一年生产a件产品,第二年比第一年增产了20%,则两年共生产产品的件数为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值.
(1)(2x2y-4xy2)-(-
 xy2+x2y),其中x=-1,y=2;
xy2+x2y),其中x=-1,y=2;(2)2x2-[3(-
 x2+
x2+ xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x-
xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x- |+(y+1)2=0.
|+(y+1)2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知多项式
 x2ym+1+xy2-2x3+8是六次四项式,单项式-
x2ym+1+xy2-2x3+8是六次四项式,单项式-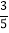 x3ay5-m的次数与多项式的次数相同,求m,a的值;
x3ay5-m的次数与多项式的次数相同,求m,a的值;(2)已知多项式mx4+(m-2)x3+(2n+1)x2-3x+n不含x2和x3的项,试写出这个多项式,再求当x=-1时多项式的值.
-
科目: 来源: 题型:
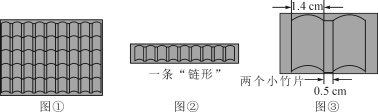
查看答案和解析>>【题目】如图①是一种竹凉席,它是由规格为1.4 cm×3 cm的小竹片按横、竖方向编织而成的.如图②是这种规格的凉席横向组成部分的一条“链形”,每相邻两个小竹片的长边互相平行,且间距为0.5 cm(如图③).
(1)5个小竹片组成的“链形”长为_____cm;
(2)n个小竹片组成的“链形”长为____cm;
(3)如果此种竹凉席的长为1.99 m,那么一条“链形”中有小竹片多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
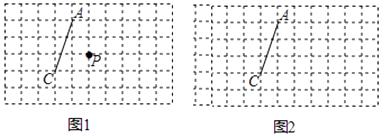
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为一条对角线、面积为15的菱形ABCD,且点B和点D均在小正方形的顶点上. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是
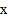 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)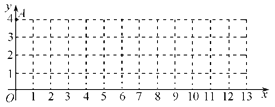
相关试题

