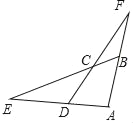
【题目】如图,已知四边形ABCD的一组对边AD、BC的延长线相交于点E.另一组对边AB、DC的延长线相交于点F,若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
参考答案:
【答案】![]()
【解析】分析:作辅助线,构建直角三角形,利用三角函数计算DH和CH的长,并设AD=5a,则DG=3a,AG=4a,证明△AFG∽△CEH,列比例式可得a的值,从而得AD的长.
详解:过C作CH⊥AD于H.
∵cos∠ADC=![]() ,CD=5,∴DH=3,∴CH=4,∴tan∠E=
,CD=5,∴DH=3,∴CH=4,∴tan∠E=![]() =
=![]() ,
,
过A作AG⊥CD于G,设AD=5a,则DG=3a,AG=4a,
∴FG=DF﹣DG=5+n﹣3a.
∵CH⊥AD,AG⊥DF.
∵∠CHE=∠AGF=90°.
∵∠ADC=∠ABC,∴∠EDC=∠CBF.
∵∠DCE=∠BCF,∴∠E=∠F,∴△AFG∽△CEH,
∴![]() ,∴a=
,∴a=![]() ,∴AD=5a=
,∴AD=5a=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a,如:min{1,-2)=-2,min{-3,-2)=-3,则方程min{x,-x}=x2-1的解是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一把直尺,
 的直角三角板和光盘如图摆放,
的直角三角板和光盘如图摆放, 为
为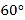 角与直尺交点,
角与直尺交点, ,则光盘的直径是( )
,则光盘的直径是( )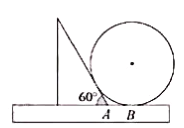
A. 3 B.
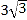 C.
C. 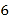 D.
D. 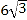
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理
 、
、 两种型号的净水器,每台
两种型号的净水器,每台 型净水器比每台
型净水器比每台 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进 型净水器与用4.5万元购进
型净水器与用4.5万元购进 型净水器的数量相等.
型净水器的数量相等.(1)求每台
 型、
型、 型净水器的进价各是多少元;
型净水器的进价各是多少元;(2)槐荫公司计划购进
 、
、 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中 型净水器为
型净水器为 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时 型净水器每台售价2500元,
型净水器每台售价2500元, 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
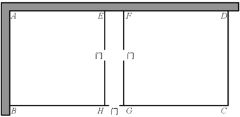
查看答案和解析>>【题目】某农场要建一个饲养场(矩形ABCD)两面靠现有墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏)。建成后木栏总长45米。设饲养场(矩形ABCD)的一边AB长为x米.
(1)饲养场另一边BC= 米(用含x的代数式表示).
(2)若饲养场的面积为180平方米,求x的值.
-
科目: 来源: 题型:
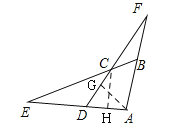
查看答案和解析>>【题目】在等腰
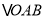 和等腰
和等腰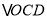 中,
中,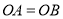 ,
,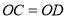 ,连接
,连接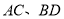 交于点
交于点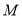 .
.(1)如图1,若
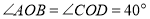 :
:①
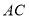 与
与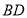 的数量关系为 ;
的数量关系为 ;②
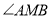 的度数为 ;
的度数为 ;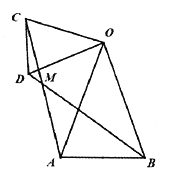
图1
(2)如图2,若
 :
: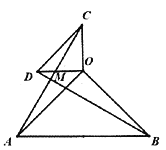
图2
①判断
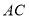 与
与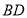 之间存在怎样的数量关系?并说明理由;
之间存在怎样的数量关系?并说明理由;②求
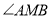 的度数;
的度数;
相关试题

