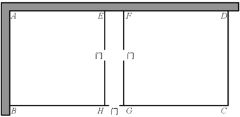
【题目】某农场要建一个饲养场(矩形ABCD)两面靠现有墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏)。建成后木栏总长45米。设饲养场(矩形ABCD)的一边AB长为x米.
(1)饲养场另一边BC= 米(用含x的代数式表示).
(2)若饲养场的面积为180平方米,求x的值.
参考答案:
【答案】(1)(48-3x);(2)10.
【解析】
(1)设饲养场(矩形ABCD)的一边(AB)长为x米,得出EH、FG所用围栏长均为(x-1)米,CD=x米,BC=45-(x+x-1+x-1)+1=48-3x(米),
(2)根据矩形面积公式可得方程;解方程即可得答案.而AB和AD长限制了x的取值.
解:(1)设饲养场(矩形ABCD)的一边(AB)长为x米,得出EH、FG所用围栏长均为(x-1)米,CD=x米,BC=45-(x+x-1+x-1)+1=48-3x(米),
![]()
![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一把直尺,
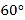 的直角三角板和光盘如图摆放,
的直角三角板和光盘如图摆放,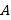 为
为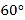 角与直尺交点,
角与直尺交点, ,则光盘的直径是( )
,则光盘的直径是( )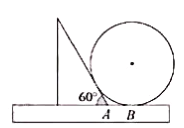
A. 3 B.
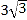 C.
C. 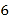 D.
D. 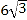
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD的一组对边AD、BC的延长线相交于点E.另一组对边AB、DC的延长线相交于点F,若cos∠ABC=cos∠ADC=
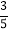 ,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).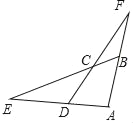
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理
 、
、 两种型号的净水器,每台
两种型号的净水器,每台 型净水器比每台
型净水器比每台 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进 型净水器与用4.5万元购进
型净水器与用4.5万元购进 型净水器的数量相等.
型净水器的数量相等.(1)求每台
 型、
型、 型净水器的进价各是多少元;
型净水器的进价各是多少元;(2)槐荫公司计划购进
 、
、 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中 型净水器为
型净水器为 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时 型净水器每台售价2500元,
型净水器每台售价2500元, 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰
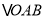 和等腰
和等腰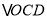 中,
中,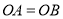 ,
,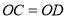 ,连接
,连接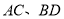 交于点
交于点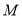 .
.(1)如图1,若
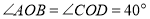 :
:①
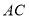 与
与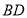 的数量关系为 ;
的数量关系为 ;②
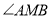 的度数为 ;
的度数为 ;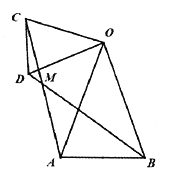
图1
(2)如图2,若
 :
: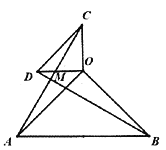
图2
①判断
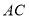 与
与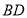 之间存在怎样的数量关系?并说明理由;
之间存在怎样的数量关系?并说明理由;②求
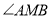 的度数;
的度数; -
科目: 来源: 题型:
查看答案和解析>>【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=
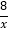 (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣
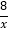 <0的x的取值范围;
<0的x的取值范围;(3)求△AOB的面积.

相关试题

