【题目】用两种方法证明“直角三角形斜边上的中线等于斜边的一半”.
已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= ![]() AB.
AB.
证法1:如图2,在∠ACB的内部作∠BCE=∠B,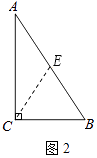
CE与AB相交于点E.
∵∠BCE=∠B,
∴ .
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵ ,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE= ![]() AB.
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD= ![]() AB.
AB.
请把证法1补充完整,并用不同的方法完成证法2.
参考答案:
【答案】EC=EB;∠A+∠B=90°
【解析】解:证法1:如图2,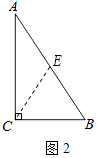
在∠ACB的内部作∠BCE=∠B,
CE与AB相交于点E.
∵∠BCE=∠B,
∴EC=EB,
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵∠A+∠B=90°,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE= ![]() AB.
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD= ![]() AB.
AB.
所以答案是:EC=EB;∠A+∠B=90°;
证法2:延长CD至点E,使得DE=CD,连接AE、BE.如图3所示: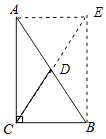
∵AD=DB,DE=CD.
∴四边形ACBE是平行四边形.
又∵∠ACB=90°,
∴四边形ACBE是矩形.
∴AB=CE,
又∵CD= ![]() CE,
CE,
∴CD= ![]() AB.
AB.
【考点精析】解答此题的关键在于理解直角三角形斜边上的中线的相关知识,掌握直角三角形斜边上的中线等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)求A、B两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.
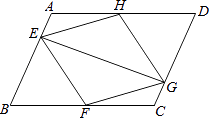
(1)求证:△AEH≌△CGF;
(2)求证:四边形EFGH是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商家用1200元购进了一批T恤,上市后很快售完,商家又用2800元购进了第二批这种T恤,所购数量是第一批购进量的2倍,但单价贵了5元.
(1)该商家购进的第一批T恤是多少件?
(2)若两批T恤按相同的标价销售,最后剩下20件按八折优惠卖出,如果希望两批T恤全部售完的利润率不低于16%(不考虑其它因素),那么每件T恤的标价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车
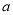 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示.
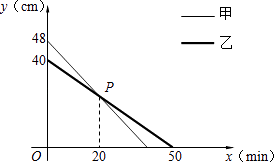
(1)求乙蜡烛剩下的长度y与燃烧时间x的函数表达式;
(2)求点P的坐标,并说明其实际意义;
(3)求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=45°, AM⊥BC,垂足为M.
(1)如图1,若AB=4
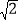 ,BC=7,求AC的长;
,BC=7,求AC的长;(2)如图2, 点D是线段AM上一点,MD=MC,点E是△ABC外一点,CE=CA,连接ED并延长交BC于点F,且∠BDF=∠CEF,
求证①AC=BD;
②BF=CF.

相关试题

