【题目】如图所示,在四边形ABCD中. 
(1)求四边形的内角和;
(2)若∠A=∠C,∠B=∠D,判断AD与BC的位置关系,并说明理由.
参考答案:
【答案】
(1)解:∠A+∠B+∠C+∠D=(4﹣2)180°=360°
(2)解:∵∠A=∠C,∠B=∠D,
∠A+∠B+∠C+∠D=360°,
∴∠A+∠B+∠A+∠B=360°,
∴2∠A+2∠B=360°
即:∠A+∠B=180°,
∴AD∥BC
【解析】(1)根据四边形的内角和即可得到结论;(2)根据四边形的内角和和已知条件得到∠A+∠B+∠A+∠B=360°,于是得到∠A+∠B=180°,根据平行线的判定定理即可得到结论.
【考点精析】认真审题,首先需要了解多边形内角与外角(多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(x+1)(x+m)的积中不含x的一次项,则m的值为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣32+(π﹣2)0+( )﹣2
)﹣2
(2)5m(﹣ abm2)(﹣a2m)
abm2)(﹣a2m)
(3)(a﹣2b)(2a+b)﹣(a+2b)2
(4)10 ×9
×9  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】正n边形的内角和等于1080,则n的值为( )
A. 7 B. 8 C. 9 D. 10
-
科目: 来源: 题型:
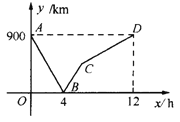
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
信息读取:(1)甲、乙两地之间的距离为
(2)请解释图中点B的实际意义;
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为( )
A.2B.3C.6D.54
-
科目: 来源: 题型:
查看答案和解析>>【题目】光的速度约为3×105km/s,以太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年的时间才能到达地球.若一年以3×107s计算,则这颗恒星到地球的距离是 km.(用科学记数法表示)
相关试题

