【题目】若关于x的一元二次方程![]() 有实数根
有实数根![]() 、
、![]() ,且
,且![]() <
<![]() ,有下列结论:①
,有下列结论:①![]() =1,
=1, ![]() =2;②
=2;②![]() ;③二次函数
;③二次函数![]() 的图象对称轴为直线x=1.5;④二次函数
的图象对称轴为直线x=1.5;④二次函数![]() 的图象与y轴交点的一定在(0,2)的上方.其中一定正确的有_________(只填正确答案的序号).
的图象与y轴交点的一定在(0,2)的上方.其中一定正确的有_________(只填正确答案的序号).
参考答案:
【答案】②③
【解析】①x1=1,x2=2是方程(x-1)(x-2)=0的两根,而代入(x-1)(x-2)=m,只有m=0时才成立,①错;②(x-1)(x-2)=m,化简整理得x2-3x+2-m=0,△=9-8+4m>0,解得m>![]() ,②正确;③由题意可得y= x2-3x+2-m,抛物线的对称轴为x=
,②正确;③由题意可得y= x2-3x+2-m,抛物线的对称轴为x=![]() ,③正确;由题意可得y= x2-3x+2-m,令x=0可得y=2-m,由②得m>
,③正确;由题意可得y= x2-3x+2-m,令x=0可得y=2-m,由②得m>![]() ,当
,当![]() 时,二次函数
时,二次函数![]() 的图象与y轴交点的在(0,2)的上方;当
的图象与y轴交点的在(0,2)的上方;当![]() 时,二次函数
时,二次函数![]() 的图象与y轴交点是(0,2);当
的图象与y轴交点是(0,2);当![]() 时,二次函数
时,二次函数![]() 的图象与y轴交点的在(0,2)的下方,所以④错误.综上,正确的结论有②③.
的图象与y轴交点的在(0,2)的下方,所以④错误.综上,正确的结论有②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分9分)已知:关于
 的方程
的方程 .
.(1)若方程有两个相等的实数根,求
 的值,并求出这时的根.
的值,并求出这时的根.(2)问:是否存在正数
 ,使方程的两个实数根的平方和等于136;若存在,请求出满足条件的
,使方程的两个实数根的平方和等于136;若存在,请求出满足条件的 值;若不存在,请说明理由.
值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)如图,在平面直角坐标系中,矩形ABCO的OA边在
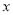 轴上,OC边在
轴上,OC边在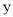 轴上,且B点坐标为(4,3).动点M、N分别从点O、B同时出发,以1单位/秒的速度运动(点M沿OA向终点A运动,点N沿BC向终点C运动),过点N作NP∥AB交AC于点P,连结MP.
轴上,且B点坐标为(4,3).动点M、N分别从点O、B同时出发,以1单位/秒的速度运动(点M沿OA向终点A运动,点N沿BC向终点C运动),过点N作NP∥AB交AC于点P,连结MP.(1)直接写出OA、AB的长度;
(2)试说明△CPN∽△CAB;
(3)在两点的运动过程中,请求出ΔMPA的面积S与运动时间
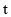 的函数关系式;
的函数关系式;(4)在运动过程中,△MPA的面积S是否存在最大值?若存在,请求出当
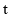 为何值时有最大值,并求出最大值;若不存在,请说明理由.
为何值时有最大值,并求出最大值;若不存在,请说明理由.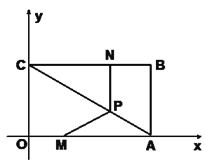
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(
 ,0)、(0,4),抛物线
,0)、(0,4),抛物线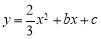 经过B点,且顶点在直线
经过B点,且顶点在直线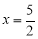 上.
上.
【1】(1)求抛物线对应的函数关系式;
【2】(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
【3】(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某报纸公布的世界人口的数据情况:
上表中的变量是( )
年份
1957
1974
1987
1999
2010
2025
人口数
30亿
40亿
50亿
60亿
70亿
80亿
A. 仅有一个是时间(年份)
B. 仅有一个是人口数
C. 有两个变量,一个是时间(年份),一个是人口数
D. 没有变量
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小李在一次高尔夫球选拔赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30o,O、A两点相距8
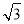 米.
米.
(1)求直线OA的解析式;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小李这一杆能否把高尔夫球从O点直接打入球洞A点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个过程中,__________的量称为常量,可以取__________的量称为变量.
相关试题

