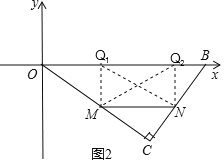
【题目】已知:如图所示,在平面直角坐标系![]() 中,
中,![]() .若点
.若点![]() 是边
是边![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 的周长与四边形
的周长与四边形![]() 的周长相等时,求
的周长相等时,求![]() 的长;
的长;
(3)在![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为等腰直角三角形?若存在,请求出此时
为等腰直角三角形?若存在,请求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

参考答案:
【答案】(1)C(16,﹣12);(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
试题分析:(1)如图1,过C作CH⊥OB于H,根据勾股定理得到BC=![]() ,根据三角形的面积公式得到CH=
,根据三角形的面积公式得到CH=![]() ,由勾股定理得到OH=
,由勾股定理得到OH=![]() ,则得到结论;
,则得到结论;
(2)∵根据相似三角形的性质得到![]() ,设CM=x,则CN=
,设CM=x,则CN=![]() x,根据已知条件列方程即可得到结论;
x,根据已知条件列方程即可得到结论;
(3)如图2,由(2)知,当CM=x,则CN=![]() x,MN=
x,MN=![]() x,①当∠OMQ1=90°MN=MQ时,②当∠MNQ2=90°,MN=NQ2时,根据相似三角形的性质即可得到结论.
x,①当∠OMQ1=90°MN=MQ时,②当∠MNQ2=90°,MN=NQ2时,根据相似三角形的性质即可得到结论.
试题解析:(1)如图1,过C作CH⊥OB于H,

∵∠C=90°,OB=25,OC=20,∴BC=![]() ,
,
∵S△OBC=![]() OBCH=
OBCH=![]() OCBC,∴CH=
OCBC,∴CH=![]() ,
,
∴OH=![]() ,∴C(16,﹣12);
,∴C(16,﹣12);
(2)∵MN∥OB,∴△CNM∽△COB,∴![]() ,
,
设CM=x,则CN=![]() x,
x,
∵△MCN的周长与四边形OMNB的周长相等,
∴CM+CN+MN=OM+MN+OB,即x+![]() x+MN=20﹣x+mn+15﹣
x+MN=20﹣x+mn+15﹣![]() x+25,
x+25,
解得:x=![]() ,∴CM=
,∴CM=![]() ;
;
(3)如图2,由(2)知,当CM=x,则CN=![]() x,MN=
x,MN=![]() x,
x,
①当∠OMQ1=90°MN=MQ时,
∵△OMQ∽△OBC,∴![]() ,
,
∵MN=MQ,∴ ,∴x=
,∴x=![]() ,
,
∴MN=![]() x=
x=![]() ×
×![]() =
=![]() ;
;
②当∠MNQ2=90°,MN=NQ2时,
此时,四边形MNQ2Q1是正方形,
∴NQ2=MQ1=MN,∴MN=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解三中九年级840名学生的体重情况,从中抽取100名学生的体重进行分析.在这项调查中,样本是指( )
A.840名学生B.被抽取的100名学生
C.840名学生的体重D.被抽取的100名学生的体重
-
科目: 来源: 题型:
查看答案和解析>>【题目】荆车中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动.为了了解学生对这四种活动的喜爱情况,学校随机调查了该校
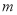 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.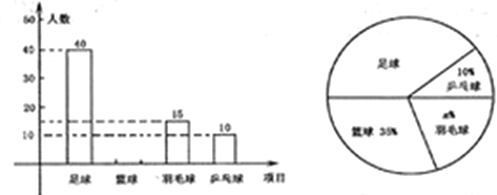
(1)
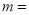 _____________,
_____________,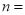 _______________;
_______________;(2)请补全上图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;
(4)在抽查的
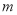 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中, ,点
,点 是
是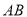 的中点,点
的中点,点 是
是 的中点,点
的中点,点 是
是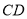 的中点,过点
的中点,过点 作
作 交
交 的延长线于点
的延长线于点 .
.
(1)求证:
 ;
;(2)若
 ,求
,求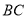 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中,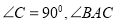 的平分线
的平分线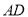 交
交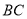 于点
于点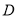 ,过点
,过点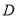 作
作 交
交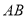 于点
于点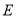 ,以
,以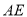 为直径作
为直径作 .
.
(1)求证:
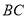 是
是 的切线;
的切线;(2)若
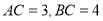 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若方程x|a|﹣1+(a﹣2)y=3是二元一次方程,则a的取值范围是( )
A.a>2
B.a=2
C.a=﹣2
D.a<﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某长途汽车站规定,乘客可以免费携带一定质量的行李,若超过该质量则需购买行李票,且行李票y(元)与行李质量x(千克)间的一次函数关系式为y=kx﹣5(k≠0),现知贝贝带了60千克的行李,交了行李费5元.
(1)若京京带了84千克的行李,则该交行李费多少元?
(2)旅客最多可免费携带多少千克的行李?
相关试题

