【题目】已知:如图,在![]() 中,
中,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
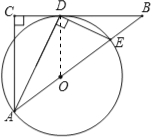
试题分析:(1)连接OD,由AE为直径、DE⊥AD可得出点D在⊙O上且∠DAO=∠ADO,根据AD平分∠CAB可得出∠CAD=∠DAO=∠ADO,由“内错角相等,两直线平行”可得出AC∥DO,再结合∠C=90°即可得出∠ODB=90°,进而即可证出BC是⊙O的切线;
(2)在Rt△ACB中,利用勾股定理可求出AB的长度,设OD=r,则BO=5﹣r,由OD∥AC可得出![]() ,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度.
,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度.
试题解析:(1)证明:连接OD,如图所示.
在Rt△ADE中,点O为AE的中心,
∴DO=AO=EO=![]() AE,∴点D在⊙O上,且∠DAO=∠ADO.
AE,∴点D在⊙O上,且∠DAO=∠ADO.
又∵AD平分∠CAB,∴∠CAD=∠DAO,∴∠ADO=∠CAD,∴AC∥DO.
∵∠C=90°,∴∠ODB=90°,即OD⊥BC.
又∵OD为半径,
∴BC是⊙O的切线;
(2)解:∵在Rt△ACB中,AC=3,BC=4,∴AB=5.
设OD=r,则BO=5﹣r.
∵OD∥AC,∴△BDO∽△BCA,
∴![]() ,即
,即![]() ,解得:r=
,解得:r=![]() ,
,
∴BE=AB﹣AE=5﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】荆车中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动.为了了解学生对这四种活动的喜爱情况,学校随机调查了该校
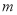 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.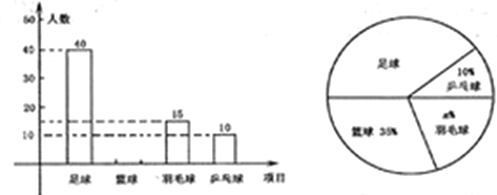
(1)
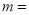 _____________,
_____________, _______________;
_______________;(2)请补全上图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;
(4)在抽查的
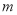 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中, ,点
,点 是
是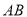 的中点,点
的中点,点 是
是 的中点,点
的中点,点 是
是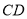 的中点,过点
的中点,过点 作
作 交
交 的延长线于点
的延长线于点 .
.
(1)求证:
 ;
;(2)若
 ,求
,求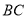 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在平面直角坐标系
 中,
中, .若点
.若点 是边
是边 上的一个动点(与点
上的一个动点(与点 不重合),过点
不重合),过点 作
作 交
交 于点
于点 .
.(1)求点
 的坐标;
的坐标;(2)当
 的周长与四边形
的周长与四边形 的周长相等时,求
的周长相等时,求 的长;
的长;(3)在
 上是否存在点
上是否存在点 ,使得
,使得 为等腰直角三角形?若存在,请求出此时
为等腰直角三角形?若存在,请求出此时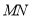 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程x|a|﹣1+(a﹣2)y=3是二元一次方程,则a的取值范围是( )
A.a>2
B.a=2
C.a=﹣2
D.a<﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某长途汽车站规定,乘客可以免费携带一定质量的行李,若超过该质量则需购买行李票,且行李票y(元)与行李质量x(千克)间的一次函数关系式为y=kx﹣5(k≠0),现知贝贝带了60千克的行李,交了行李费5元.
(1)若京京带了84千克的行李,则该交行李费多少元?
(2)旅客最多可免费携带多少千克的行李? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=
 ;④AF=
;④AF= ,其中正确结论的个数有( )
,其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个32
相关试题

