【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象. 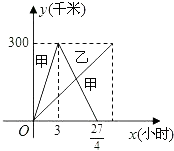
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)它们出发 ![]() 小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
参考答案:
【答案】
(1)解:当0≤x≤3时,是正比例函数,设为y=kx,
x=3时,y=300,代入解得k=100,所以y=100x;
当3<x≤ ![]() 时,是一次函数,设为y=kx+b,
时,是一次函数,设为y=kx+b,
代入两点(3,300)、( ![]() ,0),得
,0),得 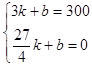
解得 ![]() ,
,
所以y=540﹣80x.
综合以上得甲车离出发地的距离y与行驶时间x之间的函数关系式 为:y= 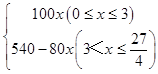 .
.
(2)解:当x= ![]() 时,y甲=540﹣80×
时,y甲=540﹣80× ![]() =180;
=180;
乙车过点( ![]() ,180),y乙=40x.(0≤x≤
,180),y乙=40x.(0≤x≤ ![]() )
)
(3)解:由题意有两次相遇.
①当0≤x≤3,100x+40x=300,解得x= ![]() ;
;
②当3<x≤ ![]() 时,(540﹣80x)+40x=300,解得x=6.
时,(540﹣80x)+40x=300,解得x=6.
综上所述,两车第一次相遇时间为第 ![]() 小时,第二次相遇时间为第6小时.
小时,第二次相遇时间为第6小时.
【解析】(1)由图知,该函数关系在不同的时间里表现成不同的关系,需分段表达.当行驶时间小于3时是正比例函数;当行使时间大于3小时小于 ![]() 小时是一次函数.可根据待定系数法列方程,求函数关系式.(2)4.5小时大于3小时,代入一次函数关系式,计算出乙车在用了
小时是一次函数.可根据待定系数法列方程,求函数关系式.(2)4.5小时大于3小时,代入一次函数关系式,计算出乙车在用了 ![]() 小时行使的距离.从图象可看出求乙车离出发地的距离y(千米)与行驶时间x(小时)之间是正比例函数关系,用待定系数法可求解.(3)两者相向而行,相遇时甲、乙两车行使的距离之和为300千米,列出方程解答,由题意有两次相遇.
小时行使的距离.从图象可看出求乙车离出发地的距离y(千米)与行驶时间x(小时)之间是正比例函数关系,用待定系数法可求解.(3)两者相向而行,相遇时甲、乙两车行使的距离之和为300千米,列出方程解答,由题意有两次相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的两边长分别是10和8,则第三边的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC中的三边长为a,b,c,若a=8,b=15,那么c2等于( )
A. 161 B. 289 C. 225 D. 161或289
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
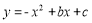 与直线
与直线 交于
交于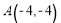 ,
,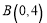 两点,直线
两点,直线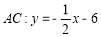 交
交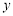 轴与点
轴与点 ,点
,点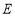 是直线
是直线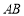 上的动点,过点
上的动点,过点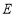 作
作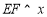 轴交
轴交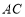 于点
于点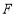 ,交抛物线于点
,交抛物线于点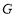 .
.(1)求抛物线
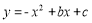 的表达式;
的表达式;(2)连接
 ,
,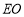 ,当四边形
,当四边形 是平行四边形时,求点
是平行四边形时,求点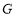 的坐标;
的坐标;(3)①在
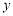 轴上存在一点
轴上存在一点 ,连接
,连接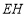 ,
,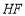 ,当点
,当点 运动到什么位置时,以
运动到什么位置时,以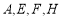 为顶点的四边形是矩形?求出此时点
为顶点的四边形是矩形?求出此时点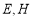 的坐标;
的坐标;②在①的前提下,以点
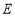 为圆心,
为圆心,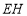 长为半径作圆,点
长为半径作圆,点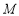 为
为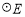 上一动点,求
上一动点,求 的最小值.
的最小值.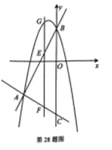
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3x2÷x=2xB.(x2)3=x5C.x3x4=x12D.2x2+3x2=5x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成直角三角形的是( )
A. 3,4,5 B. 2,3,4 C. 4,6,7 D. 5,11,12
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象过点(0,3)和(﹣2,0),那么直线必过下面的点( )
A.(4,6)
B.(﹣4,﹣3)
C.(6,9)
D.(﹣6,6)
相关试题

