【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.

(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②延长CE交BA的延长线于点F,补全图形,探究BD与EC的数量关系,并证明你的结论;
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.
参考答案:
【答案】(1)①22.5°②BD=2CE(2)BE﹣CE=2AF
【解析】试题分析:(1)①根据等腰直角三角形的性质得出∠CBA=45°,再利用角平分线的定义解答即可;②延长CE交BA的延长线于点F得出CE=FE,再利用AAS证明△ABD≌△ACF,利用全等三角形的性质解答即可;(2)过点A作AH⊥AE,交BE于点H,证明△ABH≌△ACE,进而得出CE=BH,利用等腰直角三角形的判定和性质解答即可.
试题解析:
(1)①∵在△ABC中,∠BAC=90°,AB=AC,
∴∠CBA=45°,∵BD平分∠ABC,∴∠DBA=22.5°,
∵CE⊥BD,∴∠ECD+∠CDE=90°,∠DBA+∠BDA=90°,
∵∠CDE=∠BDA,∴∠ECD=∠DBA=22.5°;
②BD=2CE.
证明:延长CE交BA的延长线于点F,如图1,
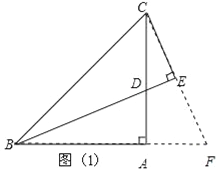
∵BD平分∠ABC,CE⊥BD,
∴CE=FE,
在△ABD与△ACF中,
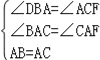 ,
,
∴△ABD≌△ACF(AAS),
∴BD=CF=2CE;
(2)结论:BE﹣CE=2AF.
证明:过点A作AH⊥AE,交BE于点H,如图2,

∵AH⊥AE,
∴∠BAH+∠HAC=∠HAC+∠CAE,
∴∠BAH=∠CAE,
在△ABH与△ACE中,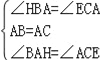 ,
,
∴△ABH≌△ACE(ASA),
∴CE=BH,AH=AE,
∴△AEH是等腰直角三角形,
∴AF=EF=HF,
∴BE﹣CE=2AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
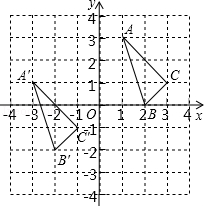
(1)分别写出下列各点的坐标:A′; B′;C′;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为;
(4)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】车库的电动门栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD的大小是( )

A.150°
B.180°
C.270°
D.360° -
科目: 来源: 题型:
查看答案和解析>>【题目】16的平方根是________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣3x2my3与2x4yn是同类项,那么m﹣n=( )
A.0
B.1
C.﹣1
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋中有红球、白球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机模出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有80次摸到红球,则口袋中红球的个数大约有( )
A.8个B.7个C.3个D.2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
相关试题

