【题目】如图,在△ABC中,AB=BC,CD⊥AB于点D,CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G,连接CG. 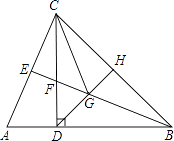
(1)求证:△ADC≌△FDB;
(2)求证:CE= ![]() BF;
BF;
(3)判断△ECG的形状,并证明你的结论;
(4)猜想BG与CE的数量关系,并证明你的结论.
参考答案:
【答案】
(1)证明:∵AB=BC,BE平分∠ABC,
∴BE⊥AC,CE=AE,
∵CD⊥AB,
∴∠ACD=∠DBF,
在△ADC和△FDB中,
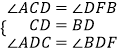 ,
,
∴△ADC≌△FDB(ASA);
(2)证明:∵△ADC≌△FDB,
∴AC=BF,
又∵CE=AE,
∴CE= ![]() BF;
BF;
(3)证明:△ECG为等腰直角三角形.
∵点H是BC边的中点,
∴GH垂直平分BC,
∴GC=GB,
∵∠DBF=∠GBC=∠GCB=∠ECF,得∠ECG=45°,
又∵BE⊥AC,
∴△ECG为等腰直角三角形;
(4)证明:GB= ![]() CE;
CE;
∵△ECG为等腰直角三角形,
∴GC= ![]() CE,
CE,
∵GC=GB,
∴GB= ![]() CE.
CE.
【解析】(1)首先根据AB=BC,BE平分∠ABC,得到BE⊥AC,CE=AE,进一步得到∠ACD=∠DBF,结合CD=BD,即可证明出△ADC≌△FDB;(2)由△ADC≌△FDB得到AC=BF,结合CE=AE,即可证明出结论;(3)由点H是BC边的中点,得到GH垂直平分BC,即GC=GB,由∠DBF=∠GBC=∠GCB=∠ECF,得∠ECO=45°,结合BE⊥AC,即可判断出△ECG的形状;(4)由△ECG为等腰直角三角形,得到GC= ![]() CE,因为GC=GB,即可得到GB=
CE,因为GC=GB,即可得到GB= ![]() CE.
CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AOB是一条直线,∠AOC=60°,OD,OE分别是∠AOC和∠BOC的平分线,则图中互补的角有( )
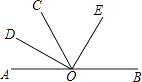
A.5对
B.6对
C.7对
D.8对 -
科目: 来源: 题型:
查看答案和解析>>【题目】若四边形ABCD中,AD=BC,AC是对角线,且∠CAD=∠ACB,则这个四边形是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】)在信宜市某“三华李”种植基地有A,B两个品种的树苗出售,已知A种比B种每株多2元,买1株A种树苗和2株B种树苗共需20元.
(1)问A,B两种树苗每株分别是多少元?
(2)为扩大种植,某农户准备购买A,B两种树苗共360株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】把一张长方形纸片ABCD按如图所示的那样折叠后,若得到∠AEB′=56°,则∠BEF= .
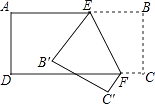
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法取近似数:π(精确到百分位)≈_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
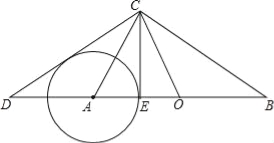
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD=
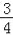 ,BC=10,求CE的长;
,BC=10,求CE的长;(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
相关试题

