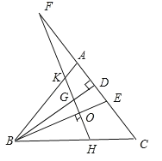
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H .下列结论:
①∠DBE=∠F;②∠F=∠BAC-∠C;
③2∠BEF=∠BAF+∠C;④∠BGH=∠ABE+∠C.其中正确的有( )
A.1B.2C.3D.4
参考答案:
【答案】C
【解析】
根据BD⊥FD,FH⊥BE和∠FGD=∠BGH,证明结论正确;
②证明∠DBE=∠BAC-∠C,根据①的结论,证明结论正确;
③根据角平分线的定义和三角形外角的性质证明结论正确;
④根据角平分线的定义和三角形外角的性质证明结论正确.
①∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,
正确;
②
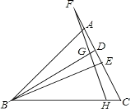
∠ABD=90°∠BAC,
∠DBE=∠ABE∠ABD=∠ABE90°+∠BAC=∠CBD∠DBE90°+∠BAC,
∵∠CBD=90°∠C,
∴∠DBE=∠BAC∠C∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC∠C∠DBE,
②错误;
③∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
③正确;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠BGH=∠ABE+∠C,
④正确,
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解七年级
 名学生其中数学考试情况,从中抽取了
名学生其中数学考试情况,从中抽取了 名学生的数学成绩进行了统计,下面
名学生的数学成绩进行了统计,下面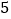 个判断中正确的有( )个.
个判断中正确的有( )个.①这种调查的方式是抽样调查;②
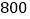 名学生是总体;③每名学生的数学成绩是个体;④
名学生是总体;③每名学生的数学成绩是个体;④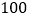 名学生是总体的一个样本;⑤样本容量是
名学生是总体的一个样本;⑤样本容量是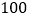 .
.A.
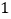 B.
B.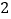 C.
C.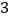 D.
D.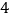
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )
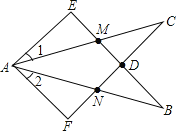
A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为( )

A. 50°B. 98°C. 75°D. 80°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而
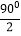 =45是360°(多边形外角和)的
=45是360°(多边形外角和)的 ,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
图2中的图案外轮廓周长是_____;
在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别
年龄段
频数(人数)
第1组

5
第2组


第3组

35
第4组
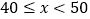
20
第5组

15

(1)请直接写出
 ,
, ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接全国文明城市创建,市交警队的一辆警车在一条东西方向的公路上巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程为:+2,-3,+2,+1,-2,-1,-2(单位:千米)
(1)最后,这辆警车的司机如何向队长描述他的位置?
(2)如果此时距离出发点东侧2千米处出现交通事故,队长命令他马上赶往现场处置,则警车在此次巡逻和处理事故中共耗油多少升?(已知每千米耗油0.2升)
相关试题

