【题目】我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,
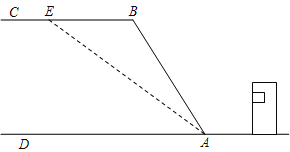
(1)求山坡高度;
(2)为防夏季因暴雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少是多少米(结果保留根号)?
参考答案:
【答案】(1)山坡的高度为20![]() 米;(2)BE至少20(
米;(2)BE至少20(![]() -1)米.
-1)米.
【解析】试题分析:(1)作BG⊥AD于G.构建直角△ABG,通过解该直角三角形求得BG的长度,即山坡高度;
(2)作EF⊥AD于F.通过解直角△ABG得到线段AG的长度,然后解直角△AEF求得AF=EF=BG=20![]() .所以BE=FG=AF-AG.
.所以BE=FG=AF-AG.
试题解析:(1)作BG⊥AD于G.
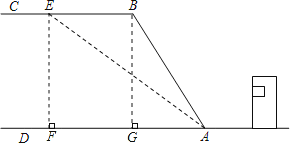
∵Rt△ABG中,∠BAD=60°,AB=40,
∴BG=AB![]() sin60°=20
sin60°=20![]() ,
,
∴山坡的高度为20![]() 米;
米;
(2)作EF⊥AD于F.
AG=AB![]() cos60°=20.
cos60°=20.
同理在Rt△AEF中,∠EAD=45°,
∴AF=EF=BG=20![]() ,
,
∴BE=FG=AF-AG=20(![]() -1)米
-1)米
∴BE至少20(![]() -1)米.
-1)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A=100°,那么∠A补角为 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC,∠A、∠B、∠C的对边分别是a、b、c,一条直线DE与边AC相交于点D,与边AB相交于点E.
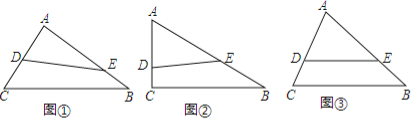
(1)如图①,若DE将△ABC分成周长相等的两部分,则AD+AE等于多少;(用a、b、c表示)
(2)如图②,若AC=3,AB=5,BC=4.DE将△ABC分成周长、面积相等的两部分,求AD;
(3)如图③,若DE将△ABC分成周长、面积相等的两部分,且DE∥BC,则a、b、c满足什么关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的坐标为 ( )
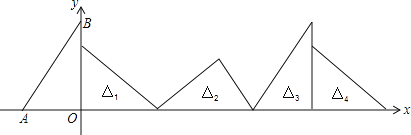
A. 8065 B. 8064 C. 8063 D. 8062
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是:( )
A. 互为相反数的两数的和为0 B. 互为相反数的两数的商为-1
C. 互为相反数的两数的平方相等 D. 互为相反数的两数的绝对值相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )
A.8或10 B.8 C.10 D.6或12
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别为4cm和8cm,则它的周长为( )
A.16cm B.17cm C.20cm D.16cm或20cm
相关试题

