【题目】如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=![]() 和y=
和y=![]() 的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为
的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为 
参考答案:
【答案】3
【解析】解:设P(0,b),
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,而点A在反比例函数y=﹣![]() 的图象上,
的图象上,
∴当y=b,x=﹣![]() , 即A点坐标为(﹣
, 即A点坐标为(﹣![]() , b),
, b),
又∵点B在反比例函数y=![]() 的图象上,
的图象上,
∴当y=b,x=![]() , 即B点坐标为(
, 即B点坐标为(![]() , b),
, b),
∴AB=![]() ﹣(﹣
﹣(﹣![]() )=
)=![]() ,
,
∴S△ABC=![]() ABOP=
ABOP=![]()
![]() b=3.
b=3.
所以答案是:3.
【考点精析】关于本题考查的比例系数k的几何意义,需要了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式a-4a分解因式,结果正确的是【 】
A.a (a-4) B. (a+2)(a-2) C. a(a+2)( a-2) D. (a-2 ) -4
-
科目: 来源: 题型:
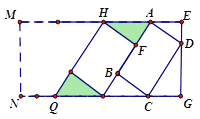
查看答案和解析>>【题目】如图,在一个矩形停车场MNGE中,矩形ABCD是一辆机动车停放的车位示意图,经测量得AB=5.4米,BC=2.4米,AF=1.8米,HF⊥AB.其中HF是另一车位的一边,所有车位尺寸一样,并按图示并列划定.
(1)求路宽EG;
(2)若停车场的长EM=85米,求这个停车场的停车车位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在数轴上点
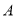 ,
, 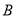 所对应的数是
所对应的数是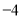 ,
, 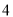 .
.对于关于
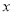 的代数式
的代数式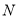 ,我们规定:当有理数
,我们规定:当有理数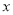 在数轴上所对应的点为
在数轴上所对应的点为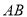 之间(包括点
之间(包括点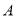 ,
, 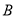 )的任意一点时,代数式
)的任意一点时,代数式 取得所有值的最大值小于等于
取得所有值的最大值小于等于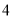 ,最小值大于等于
,最小值大于等于 ,则称代数式
,则称代数式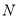 ,是线段
,是线段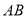 的封闭代数式.
的封闭代数式.例如,对于关于
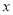 的代数式
的代数式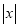 ,当
,当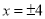 时,代数式
时,代数式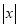 取得最大值是
取得最大值是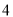 ;当
;当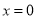 时,代数式
时,代数式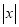 取得最小值是
取得最小值是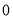 ,所以代数式
,所以代数式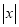 是线段
是线段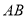 的封闭代数式.
的封闭代数式.问题:(
 )关于
)关于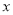 代数式
代数式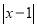 ,当有理数
,当有理数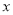 在数轴上所对应的点为
在数轴上所对应的点为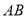 之间(包括点
之间(包括点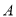 ,
, 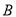 )的任意一点时,取得的最大值和最小值分别是__________.
)的任意一点时,取得的最大值和最小值分别是__________.所以代数式
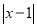 __________(填是或不是)线段
__________(填是或不是)线段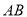 的封闭代数式.
的封闭代数式.(
 )以下关
)以下关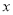 的代数式:
的代数式:①
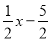 ;②
;②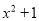 ;③
;③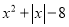 ;④
;④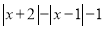 .
.是线段
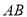 的封闭代数式是__________,并证明(只需要证明是线段
的封闭代数式是__________,并证明(只需要证明是线段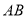 的封闭代数式的式子,不是的不需证明).
的封闭代数式的式子,不是的不需证明).(
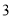 )关于
)关于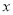 的代数式
的代数式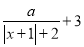 是线段
是线段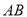 的封闭代数式,则有理数
的封闭代数式,则有理数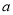 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.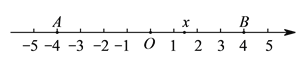
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式x2﹣1﹣2x+x3按x的升幂排列得: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从
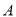 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位: 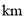 )
)第一次
第二次
第三次
第四次
第五次
第六次
第七次
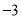
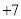
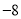
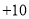
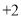
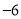
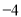
(
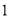 )在第__________次记录时距
)在第__________次记录时距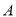 地最远.
地最远.(
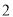 )求收工时距
)求收工时距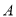 地多远?在
地多远?在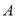 地的什么方向上?
地的什么方向上?(
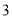 )若每
)若每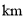 耗油
耗油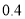 升,问共耗油多少升?
升,问共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】(-8)2018×(0.125)2019=______.
相关试题

