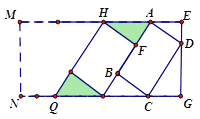
【题目】如图,在一个矩形停车场MNGE中,矩形ABCD是一辆机动车停放的车位示意图,经测量得AB=5.4米,BC=2.4米,AF=1.8米,HF⊥AB.其中HF是另一车位的一边,所有车位尺寸一样,并按图示并列划定.
(1)求路宽EG;
(2)若停车场的长EM=85米,求这个停车场的停车车位数.
参考答案:
【答案】(1)5.76m;(2)27个.
【解析】分析:(1)在直角三角形中,利用三角函数关系,由已知角度和边求得AH和PQ,而求得EG的长;(2)由 Rt△AHFRt△DAERt△CDG可得AE、CG的值,然后比较大小即可得出结果.
本题解析:(1)作QP⊥AM,则![]()
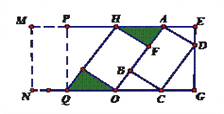
在Rt△AFH中
![]() ,
,
∵Rt△HQPRt△AHF∴![]()
∴![]() ,∴PQ=5.76m
,∴PQ=5.76m
∴EG=5.76米
(2)∵![]()
∴![]()
∴![]()
∴AE=1.92m, CG=3.24m
∴![]()
∴![]() 个,所以这个停车场有27个停车位。
个,所以这个停车场有27个停车位。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数有( )
①一元二次方程的一般形式为ax2+bx+c=0
②平分弦的直径垂直于弦,并且平分弦所对的两条弧.
③同弦或等弦所对的圆周角相等
④方程x2=x的解是x=1.
A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两条边长为1cm和3cm,则这个三角形的周长为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式a-4a分解因式,结果正确的是【 】
A.a (a-4) B. (a+2)(a-2) C. a(a+2)( a-2) D. (a-2 ) -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在数轴上点
 ,
,  所对应的数是
所对应的数是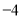 ,
, 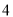 .
.对于关于
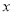 的代数式
的代数式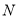 ,我们规定:当有理数
,我们规定:当有理数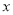 在数轴上所对应的点为
在数轴上所对应的点为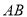 之间(包括点
之间(包括点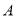 ,
, 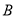 )的任意一点时,代数式
)的任意一点时,代数式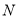 取得所有值的最大值小于等于
取得所有值的最大值小于等于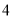 ,最小值大于等于
,最小值大于等于 ,则称代数式
,则称代数式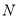 ,是线段
,是线段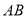 的封闭代数式.
的封闭代数式.例如,对于关于
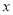 的代数式
的代数式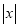 ,当
,当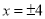 时,代数式
时,代数式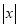 取得最大值是
取得最大值是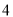 ;当
;当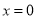 时,代数式
时,代数式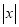 取得最小值是
取得最小值是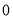 ,所以代数式
,所以代数式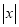 是线段
是线段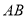 的封闭代数式.
的封闭代数式.问题:(
 )关于
)关于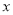 代数式
代数式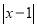 ,当有理数
,当有理数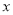 在数轴上所对应的点为
在数轴上所对应的点为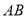 之间(包括点
之间(包括点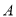 ,
, 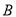 )的任意一点时,取得的最大值和最小值分别是__________.
)的任意一点时,取得的最大值和最小值分别是__________.所以代数式
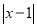 __________(填是或不是)线段
__________(填是或不是)线段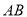 的封闭代数式.
的封闭代数式.(
 )以下关
)以下关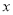 的代数式:
的代数式:①
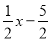 ;②
;②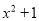 ;③
;③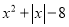 ;④
;④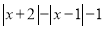 .
.是线段
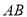 的封闭代数式是__________,并证明(只需要证明是线段
的封闭代数式是__________,并证明(只需要证明是线段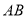 的封闭代数式的式子,不是的不需证明).
的封闭代数式的式子,不是的不需证明).(
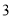 )关于
)关于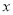 的代数式
的代数式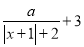 是线段
是线段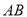 的封闭代数式,则有理数
的封闭代数式,则有理数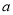 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.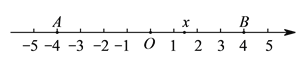
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过y轴上任意一点P,作x轴的平分线,分别于反比例函数y=
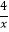 和y=
和y=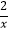 的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为
的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为 
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式x2﹣1﹣2x+x3按x的升幂排列得: .
相关试题

