【题目】作图题:(不写作法,但要保留痕迹)
(1)作出下面图形关于直线l的轴对称图形(图1). 
(2)在图2中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等. 
(3)在图3中找到一点M,使它到A、B两点的距离和最小. 
参考答案:
【答案】
(1)解:轴对称图形如图1所示;

(2)解:点A如图2所示;

(3)解:点M如图3所示.

【解析】(1)找出四边形的四个顶点关于直线l的对称点的位置,然后顺次连接即可;(2)根据角平分线上的点到角的两边的距离相等,线段垂直平分线上的点到线段两端点的距离相等分别作出∠HOF的平分线和MN的垂直平分线,交点即为A;(3)根据轴对称确定最短路径问题,作出点B关于直线的对称点B′,连接AB′与直线的交点即为点M.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a|=2,则a=( )
A.2
B.﹣2
C.2或﹣2
D.以上答案都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校有一块长为(3a+b)m,宽为(2a+b)m的长方形空地,中间是边长(a+b)m的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
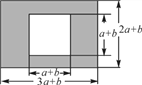
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,
,  ,点
,点 在边
在边 上,且
上,且 ,以
,以 为圆心,
为圆心,  长为半径的圆分别交
长为半径的圆分别交 ,
,  于
于 ,
,  两点.
两点.(1)求证:
 是
是 的切线;
的切线;(2)判断由
 ,
,  ,
,  及切点所构成的四边形的形状,并说明理由.
及切点所构成的四边形的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,0,﹣2,1四个数中,最小的数是( )
A.﹣1
B.0
C.﹣2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】龟兔赛跑,它们从同一地点同时出发,不久兔子就把乌龟远远地甩在后面,于是兔子便得意洋洋地躺在一棵大树下睡起觉来.乌龟一直在坚持不懈、保持一定速度地向终点跑着.兔子一觉醒来,看见乌龟快接近终点了,这才慌忙追赶上去,但最终输给了乌龟.下列图象中能大致反映龟、兔行进的路程S随时间t变化而变化的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD折叠,使C落在F处,BF交AD于E,则下列结论不一定成立的是( )
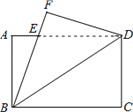
A. AD=BF B. △ABE≌FDE C.
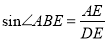 D. △ABE∽△CBD
D. △ABE∽△CBD
相关试题

