【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,以
,以![]() 为圆心,
为圆心, ![]() 长为半径的圆分别交
长为半径的圆分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点.
两点.
(1)求证: ![]() 是
是![]() 的切线;
的切线;
(2)判断由![]() ,
, ![]() ,
, ![]() 及切点所构成的四边形的形状,并说明理由.
及切点所构成的四边形的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)四边形![]() 为菱形,理由见解析.
为菱形,理由见解析.
【解析】试题分析:(1)作OF⊥AC于F,如图,理由三角函数可得到∠A=30°,OA=2OF,再利用BO=![]() AB得到OA=2OB,所以OF=OB,于是根据切线的判定方法可判AC是⊙O的切线;(2)先证明△OFD和△OBE都是等边三角形得到OD=DF,∠BOE=60°,则可计算出∠EOF=60°,从而可判定△OEF为等边三角形,所以EF=OE,则有OD=DF=EF=OE,然后根据菱形的判定方法可判断四边ODFE为菱形.
AB得到OA=2OB,所以OF=OB,于是根据切线的判定方法可判AC是⊙O的切线;(2)先证明△OFD和△OBE都是等边三角形得到OD=DF,∠BOE=60°,则可计算出∠EOF=60°,从而可判定△OEF为等边三角形,所以EF=OE,则有OD=DF=EF=OE,然后根据菱形的判定方法可判断四边ODFE为菱形.
试题解析:
(1)证明:作OF⊥AC于F,如图,
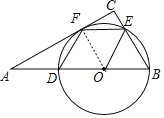
∵∠C=90°,AB=2BC,
∴sinA=![]() =
=![]() ,
,
∴∠A=30°,
∴OA=2OF,
∵BO=![]() AB,
AB,
∴OA=2OB,
∴OF=OB,
∴AC是⊙O的切线;
(2)四边形ODFE为菱形。理由如下:
∵∠A=30°,
∴∠AOF=∠B=60°,
∴△OFD和△OBE都是等边三角形,
∴OD=DF,∠BOE=60°,
∴∠EOF=180°60°60°=60°,
∴△OEF为等边三角形,
∴EF=OE,
∴OD=DF=EF=OE,
∴四边形ODFE为菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2+2x=3x的解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a|=2,则a=( )
A.2
B.﹣2
C.2或﹣2
D.以上答案都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校有一块长为(3a+b)m,宽为(2a+b)m的长方形空地,中间是边长(a+b)m的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
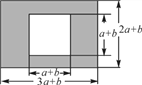
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:(不写作法,但要保留痕迹)
(1)作出下面图形关于直线l的轴对称图形(图1).
(2)在图2中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等.
(3)在图3中找到一点M,使它到A、B两点的距离和最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,0,﹣2,1四个数中,最小的数是( )
A.﹣1
B.0
C.﹣2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】龟兔赛跑,它们从同一地点同时出发,不久兔子就把乌龟远远地甩在后面,于是兔子便得意洋洋地躺在一棵大树下睡起觉来.乌龟一直在坚持不懈、保持一定速度地向终点跑着.兔子一觉醒来,看见乌龟快接近终点了,这才慌忙追赶上去,但最终输给了乌龟.下列图象中能大致反映龟、兔行进的路程S随时间t变化而变化的是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

