【题目】已知:如图,正比例函数y=ax的图象与反比例函数y= ![]() 的图象交于点C(3,1)
的图象交于点C(3,1)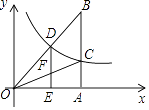
(1)试确定上述比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点D(m,n)是反比例函数图象上的一动点,其中0<m<3,过点C作直线AC⊥x轴于点A,交OD的延长线于点B;若点D是OB的中点,DE⊥x轴于点E,交OC于点F,试求四边形DFCB的面积.
参考答案:
【答案】
(1)解:将点C(3,1)分别代入y= ![]() 和y=ax,得:k=3,a=
和y=ax,得:k=3,a= ![]() ,
,
∴反比例函数解析式为y= ![]() ,正比例函数解析式为y=
,正比例函数解析式为y= ![]() x;
x;
(2)解:观察图象可知,在第二象限内,当0<x<3时,反比例函数值大于正比例函数值;
(3)解:∵点D(m,n)是OB的中点,又在反比例函数y= ![]() 上,
上,
∴OE= ![]() OA=
OA= ![]() ,点D(
,点D( ![]() ,2),
,2),
∴点B(3,4),
又∵点F在正比例函数y= ![]() x图象上,
x图象上,
∴F( ![]() ,
, ![]() ),
),
∴DF= ![]() 、BC=3、EA=
、BC=3、EA= ![]() ,
,
∴四边形DFCB的面积为 ![]() ×(
×( ![]() +3)×
+3)× ![]() =
= ![]() .
.
【解析】(1)利用待定系数法把C坐标代入解析式即可;(2)须数形结合,先找出交点,在交点的左侧与y轴之间,反比例函数值大于正比例函数值.(3)求出DF、BC、EA,代入梯形面积公式即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
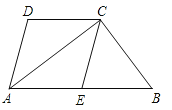
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB,CD交于点O,AC∥DB,AO=BO,E,F分别为OC,OD的中点,连接AF,BE,求证AF∥BE.
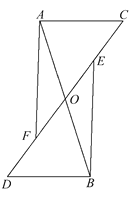
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是__________,依次继续下去……第2 016次输出的结果是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】襄江中学组织九年级部分学生到古隆中参观,租用的客车有50座和30座两种可供选择.学校根据参加参观的学生人数计算可知:若只租用30座客车x辆,还差10人才能坐满;若只租用50座客车,比只租用30座客车少用2辆,且有一辆车没有坐满但超过30人.
(1)写出九年级参观的学生人数y与x的关系式;
(2)求出此次参观的九年级学生人数;
(3)若租用一辆30座客车往返费用为260元,租用一辆50座客车往返费用为400元,如何选择租车方案费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中有三点
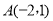 、
、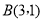 、
、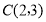 ,请回答如下问题:
,请回答如下问题:(1)在坐标系内描出点
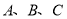 的位置:
的位置:(2)求出以
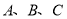 三点为顶点的三角形的面积;
三点为顶点的三角形的面积;(3)在
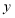 轴上是否存在点
轴上是否存在点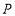 ,使以
,使以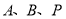 三点为顶点的三角形的面积为10,若存在,请直接写出点
三点为顶点的三角形的面积为10,若存在,请直接写出点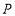 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为千米.

相关试题

