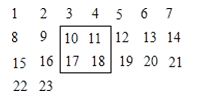
【题目】把2100个连续的正整数1、2、3、……、2100,按如图方式排列成一个数表,如图用一个正方形框在表中任意框住4个数,设左上角的数为x.
(1) 另外三个数用含x的式子表示出来,从小到大排列是___________
(2) 被框住4个数的和为416时,x值为多少?
(3) 能否框住四个数和为324?若能,求出x值;若不能,说明理由
(4) 从左到右,第1至第7列各数之和分别为a1、a2、a3、a4、a5、a6、a7,请直接写出7个数中最大的数与最小的数之差.
参考答案:
【答案】(1)x+1,x+7,x+8;(2)x=100;(3)不能;(4)1800.
【解析】试题分析:(1)根据数表的排列,可用含x的代数式表示出其它三个数;
(2)根据四个数之和为416,可得出关于x的一元一次方程,解之即可得出x的值,再由x不在第7列即可得出结论;
(3)根据四个数之和为324,可得出关于x的一元一次方程,解之即可得出x的值,再由x在第7列即可得出不存在用正方形框出的四个数的和为324;
(4)根据数表的排布,可得出总共300行其每行最右边的数比最左边的数大6,用其×300即可得出结论.
试题解析:解:(1)观察数表可知:另外三个数分别为x+1、x+7、x+8.
故答案为:x+1、x+7、x+8.
(2)设正方形框出的四个数中最小的数为x,根据题意得:x+(x+1)+(x+7)+(x+8)=416,解得:x=100.
∵100=14×7+2,∴100为第2列的数,符合题意.
答:被框住4个数的和为416时,x值为100.
(3)设正方形框出的四个数中最小的数为x,
根据题意得:x+(x+1)+(x+7)+(x+8)=324,解得:x=77,∴77=11×7,∴77为第7列的数,不符合题意,∴不存在用正方形框出的四个数的和为324.
(4)本数表共2100个数,每行7个数,共排300行,即有7列,每列共300个数,∵每一行最右边的数比最左边的数大6,∴a7﹣a1=6×(2100÷7)=1800.
答:7个数中最大的数与最小的数之差为1800.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品进价为m元,商店将价格提高30%作零售价销售.在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动.这时一件该商品的售价为( )
A.m元
B.0.8m元
C.1.04m元
D.0.92m元 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2+a2=a4
B.(a2)3=a5
C.a+2=2a
D.(ab)3=a3b3 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=kx2-x-2经过点(1,5),则k=_________.
-
科目: 来源: 题型:
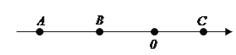
查看答案和解析>>【题目】如图,数轴上有A、B、C三个点,A、B、C对应的数分别是a、b、c,且满足
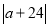 +
+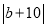 +(c-10)2=0,动点P从A出发,以每秒1个单位的速度向终点C运动,设运动时间为t秒.
+(c-10)2=0,动点P从A出发,以每秒1个单位的速度向终点C运动,设运动时间为t秒.(1)求a、b、c的值;
(2)若点P到A点的距离是点P到B点的距离的2倍,求点P对应的数;
(3)当点P运动到B点时,点Q从点A出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后第几秒时,P、Q两点之间的距离为4?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+bx+c=(x+5)(x-3),其中b,c为常数,则点P(b,c)关于y轴对称的点的坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.求证:∠BAC=∠BFC.
相关试题

