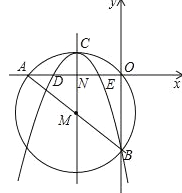
【题目】如图,在平面直角坐标系中,圆M经过原点O,且与x轴、y轴分别相交于A(﹣8,0),B(0,﹣6)两点.
(1)求出直线AB的函数解析式;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交x轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)解析式为y=﹣![]() x﹣6;(2)详见解析(3)详见解析.
x﹣6;(2)详见解析(3)详见解析.
【解析】
试题分析:(1)利用待定系数法可求出直线AB的解析式;
(2)先利用勾股定理计算出AB=10,再根据圆周角定理得到AB为⊙M的直径,则点M为AB的中点,M(﹣4,﹣3),则可确定C(﹣4,2),然后利用顶点式求出抛物线解析式;
(3)通过解方程﹣![]() (x+4)2+2=0得到D(﹣6,0),E(﹣2,0),利用S△ABC=S△ACM+S△BCM,可求出S△ABC=10,设P(t,﹣
(x+4)2+2=0得到D(﹣6,0),E(﹣2,0),利用S△ABC=S△ACM+S△BCM,可求出S△ABC=10,设P(t,﹣![]() t2﹣4t﹣6),所以
t2﹣4t﹣6),所以![]() (﹣2+6)|﹣
(﹣2+6)|﹣![]() t2﹣4t﹣6|=
t2﹣4t﹣6|=![]() 20,然后解绝对值方程求出t即可得到P点坐标.
20,然后解绝对值方程求出t即可得到P点坐标.
【试题解析】(1)设直线AB的函数解析式为y=kx+b,把A(﹣8,0),B(0,﹣6)代入得![]() ,解得
,解得 ,所以直线AB的解析式为y=﹣
,所以直线AB的解析式为y=﹣![]() x﹣6;
x﹣6;
(2)在Rt△AOB中,AB=![]() =10,∵∠AOB=90°,∴AB为⊙M的直径,
=10,∵∠AOB=90°,∴AB为⊙M的直径,
∴点M为AB的中点,M(﹣4,﹣3),∵MC∥y轴,MC=5,∴C(﹣4,2),
设抛物线的解析式为y=a(x+4)2+2,
把B(0,﹣6)代入得16a+2=﹣6,解得a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() (x+4)2+2,即y=﹣
(x+4)2+2,即y=﹣![]() x2﹣4x﹣6;
x2﹣4x﹣6;
(3)存在.
当y=0时,﹣![]() (x+4)2+2=0,解得x1=﹣2,x2=﹣4,
(x+4)2+2=0,解得x1=﹣2,x2=﹣4,
∴D(﹣6,0),E(﹣2,0),
S△ABC=S△ACM+S△BCM=![]() 8CM=20,
8CM=20,
设P(t,﹣![]() t2﹣4t﹣6),
t2﹣4t﹣6),
∵S△PDE=![]() S△ABC,
S△ABC,
∴![]() (﹣2+6)|﹣
(﹣2+6)|﹣![]() t2﹣4t﹣6|=
t2﹣4t﹣6|=![]() 20,
20,
即|﹣![]() t2﹣4t﹣6|=1,当﹣
t2﹣4t﹣6|=1,当﹣![]() t2﹣4t﹣6=1,解得t1=﹣4+
t2﹣4t﹣6=1,解得t1=﹣4+![]() ,t2=﹣4﹣
,t2=﹣4﹣![]() ,此时P点坐标为(﹣4+
,此时P点坐标为(﹣4+![]() ,1)或(﹣4﹣
,1)或(﹣4﹣![]() ,0);当﹣
,0);当﹣![]() t2﹣4t﹣6=﹣1,解得t1=﹣4+
t2﹣4t﹣6=﹣1,解得t1=﹣4+![]() ,t2=﹣4﹣
,t2=﹣4﹣![]() ;此时P点坐标为(﹣4+
;此时P点坐标为(﹣4+![]() ,﹣1)或(﹣4﹣
,﹣1)或(﹣4﹣![]() ,0).
,0).
综上所述,P点坐标为(﹣4+![]() ,1)或(﹣4﹣
,1)或(﹣4﹣![]() ,0)或(﹣4+
,0)或(﹣4+![]() ,﹣1)或(﹣4﹣
,﹣1)或(﹣4﹣![]() ,0)时,使得S△PDE=
,0)时,使得S△PDE=![]() S△ABC.
S△ABC.

-
科目: 来源: 题型:
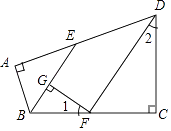
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与2互为相反数,则a+1的值为( )
A.﹣3.B.﹣1.C.1.D.3.
-
科目: 来源: 题型:
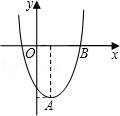
查看答案和解析>>【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
-
科目: 来源: 题型:
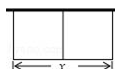
查看答案和解析>>【题目】如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计).
(1)要使鸡场面积最大,鸡场的长度应为多少米?
(2)如果中间有n(n是大于1的整数)道篱笆墙,要使鸡场面积最大,鸡场的长应为多少米?比较(1)(2)的结果,要使鸡场面积最大,鸡场长度与中间隔离墙的道数有怎样的关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD,CE相交于F.
求证:AF平分∠BAC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】截止到2019年2月19日,浙江省的注册志愿者人数达到14 480 000人. 数据14 480 000用科学记数法表示为( )
A.1.4487B.1448×104C.14.48×106D.1.448×107
相关试题

