【题目】用n边形的对角线把n边形分割成(n-2)个三角形,共有多少种不同的分割方案(n≥4)?
(探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有Pn种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?


如图①,图②,显然,只有2种不同的分割方案.所以,P4=2.



探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?
不妨把分割方案分成三类:
第1类:如图③,用A,E与B连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
第2类:如图④,用A,E与C连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为![]() 种分割方案.
种分割方案.
第3类:图⑤,用A,E与D连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
所以,P5 =![]() +
+![]() +
+![]() =
=![]() (种)
(种)




探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?
不妨把分割方案分成四类:
第1类:如图⑥,用A,F与B连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种不同的分割方案.
第2类:如图⑦,用A,F与C连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案
第3类:如图⑧,用A,F与D连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.
第4类:如图⑨,用A,F与E连接,先把六边形分割转化成1个三角形和1个五边形.再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.
所以,P6 =![]() (种)
(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则P7与P6的关系为:
P7 = ![]() ,共有_____种不同的分割方案.……
,共有_____种不同的分割方案.……
(结论)用n边形的对角线把n边形分割成(n-2)个三角形,共有多少种不同的分割方案(n≥4)?(直接写出Pn与Pn -1的关系式,不写解答过程).
(应用)用八边形的对角线把八边形分割成6个三角形,共有多少种不同的分割方案? (应用上述结论,写出解答过程)
参考答案:
【答案】18;42;![]() ;132种;
;132种;
【解析】
根据题意找到P4,P5,P6之间的关系,进行猜想,然后验证,写出答案.
P4=2,P5 =![]() ,P6=
,P6=![]() ,根据规律可得P7 =
,根据规律可得P7 =![]() =
=![]() =42,进一步推导规律:
=42,进一步推导规律: ![]() ,根据公式,P8=
,根据公式,P8=![]() =132.
=132.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
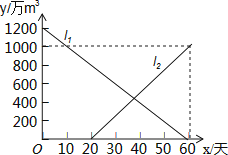
(1)求原有蓄水量y1(万m3)与时间x(天)的函数关系式,并求当x=20时的水库总蓄水量.
(2)求当0≤x≤60时,水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x的范围),若总蓄水量不多于900万m3为严重干旱,直接写出发生严重干旱时x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,l1和l2分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
(1)在刚出发时,我公安快艇距走私船多少海里?
(2)计算走私船与公安艇的速度分别是多少?
(3)求出l1,l2的解析式.
(4)问6分钟时,走私船与我公安快艇相距多少海里?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.

(1)求证:MH为⊙O的切线.
(2)若MH= ,tan∠ABC=
,tan∠ABC=  ,求⊙O的半径.
,求⊙O的半径.
(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
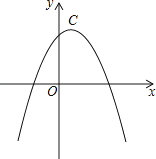
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A.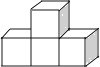
B.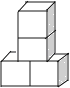
C.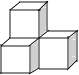
D.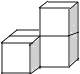
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:

(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
相关试题

