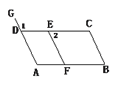
【题目】如图,点E在CD上,点F在BA上,G是AD延长线上一点.
(1 )若∠A=∠1,则可判断_______∥_______,因为________.
(2 )若∠1=∠_________,则可判断AG∥BC,因为_________.
(3 )若∠2+∠______=180°,则可判断CD∥AB,因为______
参考答案:
【答案】 AB, DC, 同位角相等,两直线平行 C 内错角相等,两直线平行 EFB 同旁内角互补,两直线平行
【解析】(1)若∠A=∠1,则可判断AB∥CD,因为“同位角相等,两直线平行”;
(2)若∠1=∠C,则可判断AG∥BC,因为“内错角相等,两直线平行”;
(3)若∠2+∠EFB=180°,则可判断CD∥AB,因为“同旁内角互补,两直线平行”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2y-4xy+4y=___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)5(x+8)﹣5=﹣6(2x﹣7)
(2)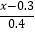 =
= 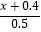 +2.
+2. -
科目: 来源: 题型:
查看答案和解析>>【题目】若x=1是关于x的方程mx-3m=2的解,则m的值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
-
科目: 来源: 题型:
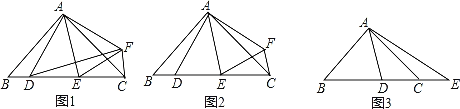
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
-
科目: 来源: 题型:
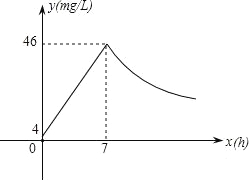
查看答案和解析>>【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图所示,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
相关试题

