【题目】如图1,已知双曲线y= ![]() (k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(1)若点A的坐标为(3,1),则点B的坐标为;当x满足:时, ![]() ≤k′x;
≤k′x;
(2)如图2,过原点O作另一条直线l,交双曲线y= ![]() (k>0)于P,Q两点,点P在第一象限.
(k>0)于P,Q两点,点P在第一象限.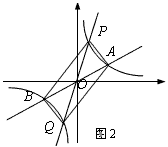
四边形APBQ一定是;
(3)若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.
(4)设点A,P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m,n应满足的条件;若不可能,请说明理由.
参考答案:
【答案】
(1)(﹣3,﹣1);﹣3≤x<0或x≥3
(2)平行四边形
(3)
∵点A的坐标为(3,1),
∴k=3×1=3,∴反比例函数的解析式为y= ,∵点P的横坐标为1,∴点P的纵坐标为3,∴点P的坐标为(1,3),
由双曲线关于原点对称可知,点Q的坐标为(﹣1,﹣3),点B的坐标为(﹣3,﹣1),
如图2,过点A、B分别作y轴的平行线,过点P、Q分别作x轴的平行线,分别交于C、D、E、F,
则四边形CDEF是矩形,
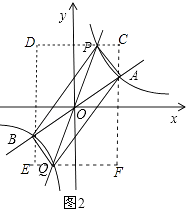
CD=6,DE=6,DB=DP=4,CP=CA=2,
则四边形APBQ的面积=矩形CDEF的面积﹣△ACP的面积﹣△PDB的面积﹣△BEQ的面积﹣△AFQ的面积
=36﹣2﹣8﹣2﹣8=16.
(4)
解:mn=k时,四边形APBQ是矩形,不可能是正方形,理由:当AB⊥PQ时四边形APBQ是正方形,此时点A、P在坐标轴上,由于点A,P可能达到坐标轴故不可能是正方形,即∠POA≠90°.因为mn=k,易知P、A关于直线y=x对称,所以PO=OA=OB=OQ,所以四边形APBQ是矩形.
【解析】解:(1)∵A、B关于原点对称,A(3,1),
∴点B的坐标为(﹣3,﹣1).由图象可知,当﹣3≤x<0或x≥3时, ![]() ≤k′x.
≤k′x.
故答案为(﹣3,﹣1),﹣3≤x<0或x≥3;(2)∵A、B关于原点对称,P、Q关于原点对称,
∴OA=OB,OP=OQ,∴四边形APBQ是平行四边形.故答案为:平行四边形;
=36﹣2﹣8﹣2﹣8=16.
(1)根据正比例函数与反比例函数的图象的交点关于原点对称,即可解决问题,利用图象根据正比例函数的图象在反比例函数的图象的上方,即可确定自变量x的范围.(2)利用对角线互相平分的四边形是平行四边形证明即可.(3)利用分割法求面积即可.(3)根据矩形的性质、正方形的性质即可判定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
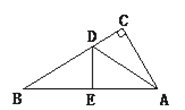
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
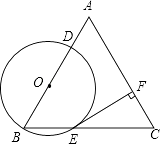
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F B. BC∥EF C. ∠A=∠EDF D. AD=CF
相关试题

