【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.

参考答案:
【答案】(1)AC=![]() ,AB=
,AB=![]() ,BC=
,BC=![]() ;(2)点C到AB的距离是
;(2)点C到AB的距离是![]() ;(3)△ABC的面积是3.5.
;(3)△ABC的面积是3.5.
【解析】
(1) 根据勾股定理可求出AC,AB,BC的长;
(3)利用正方形的面积减去三角形三个顶点上三角形的面积即可;
(2)先根据勾股定理求出AB的长,再由三角形的面积公式即可得出点C到AB的距离.
(1)AC=![]() =
=![]() ,
,
AB=![]() =
=![]() ,
,
BC=![]() =
=![]() ;
;
(2)S△ABC=3×3﹣![]() ×3×1﹣
×3×1﹣![]() ×2×1﹣
×2×1﹣![]() ×2×3=3.5,
×2×3=3.5,
设点C到AB边的距离为h,则![]() ×h×AB=3.5,
×h×AB=3.5,
解得:h=![]() .
.
即点C到AB的距离是![]() ;
;
(3)由(2)可知△ABC的面积=3.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
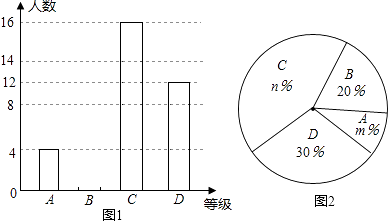
(1)参加朗诵比赛的学生共有人,并把条形统计图补充完整;
(2)扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
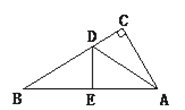
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知双曲线y=
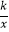 (k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(1)若点A的坐标为(3,1),则点B的坐标为;当x满足:时,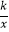 ≤k′x;
≤k′x;
(2)如图2,过原点O作另一条直线l,交双曲线y=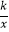 (k>0)于P,Q两点,点P在第一象限.
(k>0)于P,Q两点,点P在第一象限.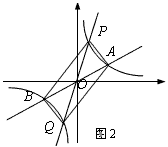
四边形APBQ一定是;
(3)若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.
(4)设点A,P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m,n应满足的条件;若不可能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
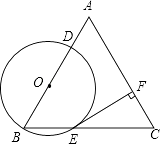
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
相关试题

