【题目】计算题:
(1) ![]() ;
;
(2) (-2x2y+6x3y4-8xy)÷(-2xy);
(3)先化简,再求值:![]() ,其中
,其中![]() .
.
参考答案:
【答案】(1) 3;(2) x-3x2y3+4;(3) 9x-5,-8.
【解析】
(1)按顺序先分别进行负指数幂的运算、立方的运算、绝对值的化简、0指数幂的运算,然后再按运算顺序进行计算即可;
(2)根据多项式除以单项式的法则进行计算即可;
(3)先利用平方差公式、单项式乘多项式法则、完全平方公式进行展开,然后合并同类项,最后把数值代入进行计算即可.
(1)原式=9-8+3-1=3;
(2)原式=-2x2y÷(-2xy)+6x3y4÷(-2xy)-8xy÷(-2xy)=x-3x2y3+4;
(3)原式=9x2-4-5x2+5x-4x2+4x-1=9x-5,
当x=![]() 时,原式=-3-5=-8.
时,原式=-3-5=-8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B均在函数
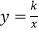 (k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
A.(2,2)
B.(2,3)
C.(3, 2)
D.(4, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上一点,∠AOD=120,∠AOC=90,OE平分∠BOD,则图中互为补角的角有__________对。

-
科目: 来源: 题型:
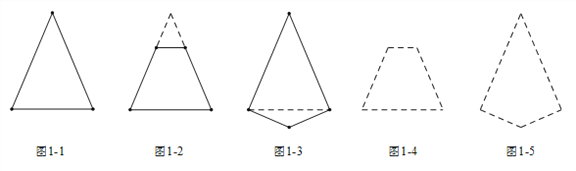
查看答案和解析>>【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有________条对称轴,非正方形的长方形有________条对称轴,等边三角形有___________条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1-2和图1-3都可以看作由图1-1修改得到的,仿照类似的修改方式,请你在图1-4和图1-5中,分别修改图1-2和图1-3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
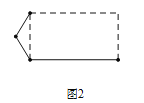
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
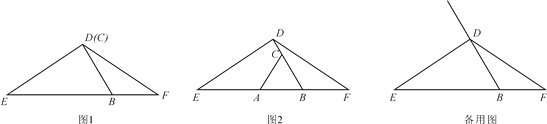
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为________;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系,不用证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
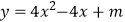 的图像与x轴的交点坐标为
的图像与x轴的交点坐标为 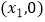
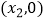 且
且 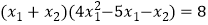 ,则该函数的最小值是( )
,则该函数的最小值是( )
A.2
B.-2
C.10
D.-10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

相关试题

