【题目】如图(1),在矩形ABCD中,AB=3,BC=4,连接BD.现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上,一条直角边过点C,另一条直角边与AB所在的直线交于点G.

(1)是否存在这样的点P,使点P、C、G为顶点的三角形与△GCB全等?若存在,画出图形,并直接在图形下方写出BG的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)
(2)如图(2),当点P在BD的延长线上时,以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F,连EF,分别过点G、C作GM⊥EF,CN⊥EF,M、N为垂足.试探究PM与FN的关系.
参考答案:
【答案】(1)BG=3;见解析(2)PM=FN.
【解析】
试题分析:(1)只需分点G在线段AB上(如图①)、在线段AB的延长线上(如图②)、在线段AB的反向延长线上(如图③)三种情况讨论,即可解决问题;
(2)如图2,由(1)可知,此时BG=PG=![]() ,BC=PC=4.易证△PGM∽△CPN,从而可得PM=
,BC=PC=4.易证△PGM∽△CPN,从而可得PM=![]() CN;易证△FNC∽△BCD,从而可得FN=
CN;易证△FNC∽△BCD,从而可得FN=![]() CN,即可得到PM=FN.
CN,即可得到PM=FN.
解:(1)存在点P,使点P、C、G为顶点的三角形与△GCB全等.
①若点G在线段AB上,如图①.

当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,
此时∠GCB=∠CGP,
∴PG∥BC,
∴∠GPC+∠PCB=90°.
∵∠GPC=90°,
∴∠PCB=90°,
∴点P在点D处,
∴BG=PC=DC=AB=3;
②若点G在线段AB的延长线上,如图②.
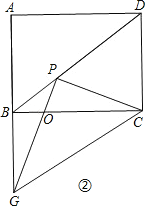
当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,
此时BC=PG,∠GCB=∠CGP,
∴OG=OC,OB=OP,
∴∠PBO=∠BPO=![]() (180°﹣∠BOP),
(180°﹣∠BOP),
∠OCG=∠OGC=![]() (180°﹣∠GOC).
(180°﹣∠GOC).
∵∠BOP=∠GOC,
∴∠PBO=∠OCG,
∴BD∥CG.
∵四边形ABCD是矩形,
∴AB∥DC,即BG∥DC,
∴四边形BGCD是平行四边形,
∴BG=CD=3;
③若点G在线段AB的反向延长线上,如图③.

当PC=BC时,根据HL可得Rt△GBC≌Rt△GPC,
此时BG=PG,
∴点G、C在BP的垂直平分线上,
∴GC垂直平分BP,
∴∠BGC+∠GBD=90°.
∵∠CBD+∠GBD=90°,
∴∠BGC=∠CBD.
又∵∠GBC=∠BCD=90°,
∴△GCB∽△BDC,
∴![]() =
=![]() .
.
∵BC=4,CD=3,
∴![]() =
=![]() ,
,
∴BG=![]() ;
;
(2)如图2,

由(1)可知,此时△GBC≌△GPC,且BG=PG=![]() ,BC=PC=4.
,BC=PC=4.
∵GM⊥EF,CN⊥EF,
∴∠GMP=∠PNC=90°,
∴∠MGP+∠GPM=90°.
∵∠GPC=90°,
∴∠GPM+∠NPC=90°,
∴∠MGP=∠NPC,
∴△PGM∽△CPN,
∴![]() =
=![]() .
.
∴![]() =
=![]() =
=![]() ,即PM=
,即PM=![]() CN.
CN.
∵PB=PF,∴∠F=∠PBC.
又∵∠FNC=∠BCD=90°,
∴△FNC∽△BCD,
∴![]() =
=![]() .
.
∵BC=4,DC=3,
∴![]() =
=![]() ,
,
∴FN=![]() CN,
CN,
∴PM=FN.
-
科目: 来源: 题型:
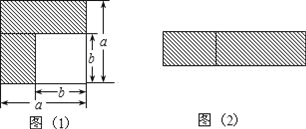
查看答案和解析>>【题目】(1)如图1,在边长为a的正方形中,画出两个长方形阴影,则阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的长是 ,宽是 ,面积是 (写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式计算:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值(a+b)2﹣(b﹣a)2﹣2(b﹣a)(b+a),其中a=1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2+x2=x4
B.x2y﹣2x2y=﹣x2y
C.(3x)2=3x2
D.x2x3=x6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )

A.
 B.
B.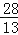 C.
C.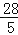 D.
D.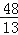
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
相关试题

