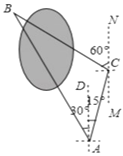
【题目】小明同学要测量公园内被湖水隔开的两颗大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°的方向.
(1)求∠ABC的度数;
(2)求两棵大树A和B之间的距离(结果精确到1米;参考数据![]() ,
, ![]() ,
, ![]() ).
).
参考答案:
【答案】两棵大树A和B之间的距离约为386米
【解析】试题分析:(1)先利用平行线的性质得∠ACM=∠DAC=15°,再利用平角的定义计算出∠ACB=105°,然后根据三角形内角和计算∠ABC的度数;
(2)作CH⊥AB于H,如图,易得△ACH为等腰直角三角形,则AH=CH=![]() AC=100
AC=100![]() ,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=
,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=![]() CH=100
CH=100![]() ,AB=AH+BH=100
,AB=AH+BH=100![]() +100
+100![]() ,然后进行近似计算即可.
,然后进行近似计算即可.
试题解析:由题意可知:∠BAC=∠BAD+∠CAD=30°+15°=45°,∠MCA=∠CAD=15°,
∴∠ACB=180°-∠MCA-∠BCN=180°-15°-60°=105°
在△ABC中,∠ABC=180°-∠BCA-∠BAC=180°-105°-45°=30°;
从点C作CH⊥AB于点H
. 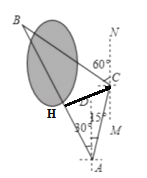
在Rt△ACH中,∵AC=200(米),∠CAH=45°,
∴CH=ACsin∠CAH=200×sin45°=200×![]() =100
=100![]() (米)
(米)
∴AH=CH=100![]() (米)
(米)
在Rt△BCH中,∵CH=100![]() (米),∠CBH=30°,
(米),∠CBH=30°,
∴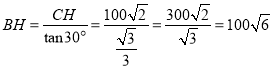 ;
;
∴AB=AH+BH=100![]() +100
+100![]() ≈386(米)
≈386(米)
答:两棵大树A和B之间的距离约为386米
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段EF是由线段PQ平移得到的,点P(-1,4)的对应点为E(4,7),则点Q(-3,1)的对应点F的坐标为( )
A. (-8,-2) B. (-2,2) C. (2,4) D. (-6,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(﹣1,﹣2),将OA绕原点O逆时针旋转180°得到OA′,点A′的坐标为(a,b),则a﹣b等于( )
A.1
B.﹣1
C.3
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】43的底数是 , 指数是 , 计算的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲看乙的方向是北偏东40°,那么乙看甲的方向是_____度.
-
科目: 来源: 题型:
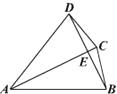
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号(把你认为正确结论的序号都填上)
相关试题

