【题目】已知A,B两地相距50千米,某日下午甲、乙两人分别骑自行车和骑摩托车从A地出发驶往B地如图所示,图中的折线PQR和线段MN分别表示甲、乙两人所行驶的路程S(千米)与该日下午时间t(时)之间的关系.请根据图象解答下列问题:
(1)直接写出:甲骑自行车出发 小时后,乙骑摩托车才开始出发;乙骑摩托车比甲骑自行车提前 小时先到达B地;
(2)求出乙骑摩托车的行驶速度;甲骑自行车在下午2时至5时的行驶速度;
(3)当甲、乙两人途中相遇时,直接写出相遇地与A地的距离.

参考答案:
【答案】(1)1,2,;(2)乙骑摩托的行驶速度为50千米/小时;甲骑自行车在下午2时至5时的行驶速度10千米/小时,(3)25千米.
【解析】
(1)认真分析图象得到甲比乙早出发的时间与乙比甲早到达的时间;
(2)速度=路程÷时间,根据图象中提供数据计算即可;
(3)甲乙相遇时即是O点的位置,设此时乙出发了t小时,可列出关于t的一元一次方程,从而求出相遇第与A的距离.
(1)由图象可知:甲从1时开始出发,乙从2时开始出发,
2﹣1=1,
故甲骑车出发1小时后,乙骑摩托车才开始出发,
由图象可知:乙在3时时到达,甲在5时时到达,
5﹣3=2,
故乙骑摩托车比甲骑自行车提前2小时先到达B地,
故答案为:1,2;
(2)由图象可知:乙的行驶路程为50千米,时间为3﹣2=1小时,
乙骑摩托的行驶速度为50÷1=50千米/小时,
甲骑自行车在下午2时至5时的行驶路程为Q﹣R的距离,
50﹣20=30千米,
时间为5﹣2=3小时,
甲骑自行车在下午2时至5时的行驶速度为30÷3=10千米/小时,
答:乙骑摩托的行驶速度为50千米/小时;甲骑自行车在下午2时至5时的行驶速度10千米/小时;
(3)设相遇时乙出发了t小时,此时二者行驶距离相同,
20+10t=50t,
解得:t=0.5小时,
此时距离A地的距离为乙的行驶距离50×0.5=25千米,
答:当甲、乙两人途中相遇时,相遇地与A地的距离为25千米,
故答案为25千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠A=52°,若∠ABC与∠ACB的角平分线交于点D1,得到∠D1,∠ABD1与∠ACD1的角平分线交于点D2,得到∠D2;依此类推,∠ABD4与∠ACD4的角平分线交于点D5,得到∠D5,则∠D5的度数是_____.

-
科目: 来源: 题型:
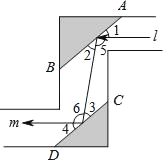
查看答案和解析>>【题目】如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?
请把下列解题过程补充完整.
理由:
因为AB∥CD,
根据“ ”,
所以∠2=∠3.
因为∠1=∠2,∠3=∠4,
所以∠1=∠2=∠3=∠4,
所以180°﹣∠1﹣∠2=180°﹣∠3﹣∠4,
即: .
根据“ ”,
所以l∥m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,一次函数
中,一次函数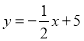 的图象
的图象 分别与
分别与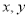 轴交于
轴交于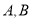 两点,正比例函数的图象
两点,正比例函数的图象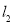 与
与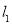 交于点
交于点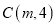
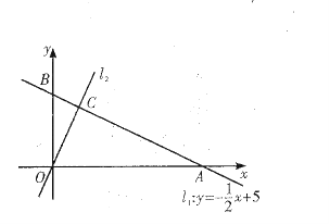
(1)求
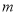 的值及
的值及 的解析式;
的解析式;(2)求
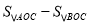 的值;
的值;(3)一次函数
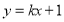 的图象为
的图象为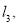 且
且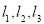 不能围成三角形,直接写出
不能围成三角形,直接写出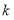 的值.
的值.
相关试题

