【题目】如图,∠AOB=30°,点P位于∠AOB内,OP=3,点M,N分别是射线OA、OB边上的动点,当△PMN的周长最小时,则∠MPN的度数为__________°.

参考答案:
【答案】120
【解析】
要求∠NPM的度数,要在△NPM中进行,根据轴对称的性质和等腰三角形的性质可证∠CPN=∠C,∠DPM=∠D,然后证明∠C+∠D=∠AOB,利用四边形内角和可得答案.
解:作P关于OB、OA的对称点C、D,连接CD交OB、OA于N、M.
此时△PNM周长有最小值;

∵P关于OB、OA的对称点C、D,,
∴OB垂直平分PC,OA垂直平分PD,
∴CN=PN,PM=DM,
∴∠CPN=∠C,∠DPM=∠D,
∵∠PRN=∠PTM=90°,
∴∠ONM=∠BNC=90-∠C, ∠OMN=∠BMD=90°-∠D,
∵∠ONM+∠OMN+∠AOB=180°,
∴90-∠C+90°-∠D+∠AOB=180°,
∴∠C+∠D=∠AOB,
∴∠CPN+∠DPM=∠AOB=30°,
在四边形OTPR中,
∴∠CPD+∠BOA=180°,
∵∠NPM+∠CPN+∠DPM+∠AOB =180°,
∴∠NPM=180°-30°-30°∠=120°.
故答案为120.
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴

解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形
 是菱形,
是菱形, 是正三角形,
是正三角形, 、
、 分别在
分别在 、
、 上,且
上,且 ,则
,则 ____度.
____度.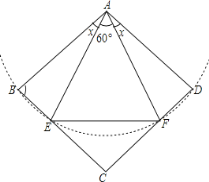
-
科目: 来源: 题型:
查看答案和解析>>【题目】从不同的方向看同一物体时,可能看到不同的图形.其中,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫俯视图.由若干个(大于
 个)大小相同的正方体组成一个几何体的主视图和俯视图如图所示,则这个几何体的左视图不可能是( )
个)大小相同的正方体组成一个几何体的主视图和俯视图如图所示,则这个几何体的左视图不可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)②图中阴影部分的面积为___________;
(2)观察图②,请你写出式子
 、
、 、
、 之间的等量关系是_________;
之间的等量关系是_________;(3)若
 ,
, ,则
,则 ______________;
______________;(4)实际上有许多恒等式可以用图形的面积来表示.如图③,它表示等式:____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.
(1)如图1,直接写出∠ABD的大小(用含α的式子表示);
(2)如图2,若∠BCE=150°,∠ABE=60°, ∠DEC=45°,求α的值;
(3)如图3,若∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形
 中,
中, 、
、 分别是边
分别是边 、
、 的中点,
的中点, 分别交
分别交 、
、 于
于 、
、 .请判断下列结论:
.请判断下列结论: ;
; ;
; ;
; .其中正确的结论有( )
.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

