【题目】如图,在平面直角坐标系中,已知![]() ,
, ![]() ,
, ![]() 三点,其中
三点,其中![]() 满足关系式
满足关系式![]() .
.
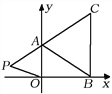
(1)求![]() 的值;
的值;
(2)如果在第二象限内有一点![]() ,那么请用含
,那么请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积与三角形
的面积与三角形![]() 的面积相等?若存在,求出点
的面积相等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)a=2,b=3,c=4;(2) ![]() ;(3)存在,点P的坐标为
;(3)存在,点P的坐标为![]() .
.
【解析】试题分析:(1)根据非负数的性质:若几个非负数的和为0,这几个数均为0,即可求得结果;
(2)过点p作PD⊥y轴于点D,由S四边形ABOP=S△AOB+S△AOP,根据三角形的面积公式求解即可;
(3)由S四边形ABOP=S△AOB+S△AOP可得S四边形ABOP=2S△AOB ,即可得到关于m的方程,再解出即可.
试题解析:(1)由![]() ,得a-2=0,b-3=0,c-4=0,∴a=2,b=3,c=4;
,得a-2=0,b-3=0,c-4=0,∴a=2,b=3,c=4;
(2)![]()
![]() ;
;
(3)存在
![]() ,
,
∴点P的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
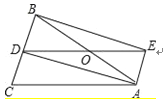
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市为促销,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元;打折后,买50件A商品和40件B商品仅需364元,这比打折前少花多少钱?
-
科目: 来源: 题型:
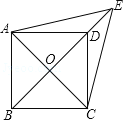
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有30个,黑球有n个.随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出的黑球的频率稳定在0.4附近,则n的值约为( )
A. 20 B. 30 C. 40 D. 50
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 2a+3b=5ab B. 2a﹣3b=﹣1 C. 2a2b﹣2ab2=0 D. 2ab﹣2ba=0
相关试题

