【题目】如图,在△ABC中,∠B=100° ,按要求完成画图并解答问题:

(1)画出△ABC的高CE,中线AF,角平分线BD,且AF所在直线交CE于点H,BD与AF相交于点G;
(2)若∠FAB=40°,求∠AFB的度数和∠BCE的度数.
参考答案:
【答案】(1)答案见解析;(2)∠AFB=40°,∠BCE=10°.
【解析】
(1)根据三角形高、中线和角平分线的定义画图;
(2)在△AFB中利用三角形内角和定理求出∠AFB的度数,然后在△BCE中利用三角形外角性质得出∠BCE的度数.
解:(1)如图,CE、AH、BD即为所求;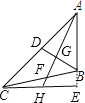
(2)在△ABF中,∠AFB=180°-∠FAB-∠ABF=180°-40°-100°=40°;
∵CE⊥AB,
∴∠BEC=90°,
∵∠ABC=∠BEC+∠BCE,
∴∠BCE=100°-90°=10°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知A(0,a)、B(b, 0),且a、b满足:
 ,点D为x正半轴上一动点
,点D为x正半轴上一动点 (1)求A、B两点的坐标
(2)如图,∠ADO的平分线交y轴于点C,点 F为线段OD上一动点,过点F作CD的平行线交y轴于点H,且∠AFH=45°, 判断线段AH、FD、AD三者的数量关系,并予以证明

(3)以AO为腰,A为顶角顶点作等腰△ADO,若∠DBA=30°,直接写出∠DAO的度数

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是________;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是________;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,△ABE与△DEF相似吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某快递公司计划购买A型和B型两种货车共8辆,其中每辆车的价格以及每辆车的运载量如下表:
A型
B型
价格(万元/台)
m
n
运载量(吨/车)
20
30
若购买A型货车1辆,B型货车3辆,共需67万元;若购买A型货车3辆,B型货车2辆,共需75万元.
(1)求m,n的值;
(2)若每辆A型货车每月运载量500吨,每辆B型货车每月运载量750吨,为确保这8辆车每月的运载量总和不少于4750吨,且该公司购买A型和B型货车的总费用不超过124万元.请你设计一个方案,使得购车总费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.

(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;
(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.
相关试题

