【题目】如图,把含![]() 角的两块直角三角板放置在同一平面内,若
角的两块直角三角板放置在同一平面内,若![]() 则以
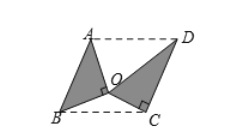
则以![]() 为顶点的四边形的面积是_____.
为顶点的四边形的面积是_____.
参考答案:
【答案】![]()
【解析】
延长CO,交AB于点E,根据平行四边形的判定可得四边形ABCD为平行四边形,然后根据平行四边形的面积公式和三角形的面积公式证出S平行四边形ABCD=2(S△AOB+S△COD),再求出OA、OB和OC,即可求出S△AOB和S△COD,从而求出结论.
解:延长CO,交AB于点E,由题意可知:∠BAO=45°,∠CDO=30°

∵![]()
∴四边形ABCD为平行四边形
∵OC⊥CD
∴CE⊥AB
∴S△AOB+S△COD=![]() AB·OE+
AB·OE+![]() CD·OC
CD·OC
=![]() AB·(OE+OC)
AB·(OE+OC)
=![]() AB·CE
AB·CE
=![]() S平行四边形ABCD
S平行四边形ABCD
∴S平行四边形ABCD=2(S△AOB+S△COD)
在Rt△AOB中,AO2+BO2=AB2=6,AO=BO
解得:AO=BO=![]()
在Rt△COD中,∠CDO=30°,OC2+CD2=OD2
∴OD=2OC, OC2+6=(2OC)2
解得:OC=![]() ,
,
∴S△AOB=![]() AO·BO=
AO·BO=![]() ,S△COD=
,S△COD=![]() CD·OC=
CD·OC=![]()
∴S平行四边形ABCD=2(S△AOB+S△COD)
=2×(![]() +
+![]() )
)
=![]()
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给定关于
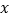 的二次函数
的二次函数  ,
,
学生甲:当 时,抛物线与
时,抛物线与 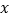 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与 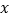 轴只有一个交点时,
轴只有一个交点时, 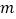 的值为3;
的值为3;
学生乙:如果抛物线在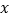 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由. -
科目: 来源: 题型:
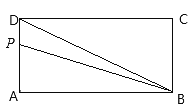
查看答案和解析>>【题目】如图,长方形ABCD中,AB=2cm,BC=4cm,点P按照顺时针方向由点A运动到点D,设点P运动的路程为
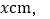 图中点P、B、D围成的图形的面积为
图中点P、B、D围成的图形的面积为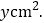
(1)写出点P、B、D围成的图形的面积
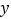 与
与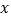 之间的关系式和自变量
之间的关系式和自变量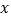 的取值范围;
的取值范围;(2)当
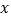 取何值时,点P、B、D围成的图形的面积等于
取何值时,点P、B、D围成的图形的面积等于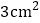 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,边长为
中,边长为 的等边三角形
的等边三角形 的顶点
的顶点 分别在
分别在 和
和 上,下列结论:
上,下列结论:


 ,其中正确的序号是( )
,其中正确的序号是( )
A.①②④B.①②C.②③④D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成以下问题:
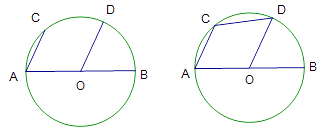
图1 图2
(1)如图1, ,弦
,弦  与半径
与半径  平行,求证:
平行,求证:  是⊙
是⊙  的直径;
的直径;
(2)如图2, 是⊙
是⊙  的直径,弦
的直径,弦  与半径
与半径  平行.已知圆的半径为
平行.已知圆的半径为  ,
,  ,
,  ,求
,求  与
与  的函数关系式.
的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的
 名选手的复赛成绩如图所示.
名选手的复赛成绩如图所示.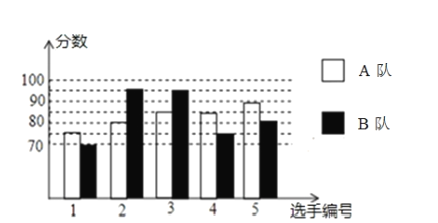
(1)根据图示补全下表;
平均数(分)
中位数(分)
众数(分)
 队
队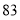
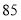
 队
队
(2)结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好;
(3)计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
相关试题

