【题目】已知一个零刻度落在点A的量角器(半圆O)的直径为AB,等腰直角△BCD绕点B旋转.
(1)如图1,当等腰直角△BCD运动至斜边BD交量角器边缘于点G,直角边CD交量角器边缘于点E,F,第三边交量角器边缘于点H时,点G在量角器上的读数为20°,求此时点H在量角器上的读数.
(2)如图2,当点G,E在量角器上的读数α,β满足什么关系时,等腰直角△BCD的直角边CD会与半圆O相切于点E?请说明理由.

参考答案:
【答案】(1)、110°;(2)、β=![]() α+45°
α+45°
【解析】
试题分析:(1)、连接OG、OH.由题意可知:∠AOG=20°,由等腰直角三角形的性质可求得∠CBD=45°,接下来,依据圆周角定理可求得∠HOG=90°,最后依据∠AOH=∠AOG+∠GOH求解即可;(2)、连接OG、OE.先由切线的性质证明OE⊥DC,然后依据平行线的判定定理可证明EO∥CB,接下来依据平行线的性质和可得到∠EOA=∠CBA,最后结合圆周角定理以及∠ABC、∠ABG、∠DBC的关系可得到α、β的关系.
试题解析:(1)、如图1所示:连接OG、OH.
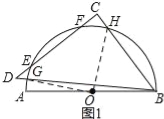
∵点G在量角器上的读数为20°, ∴∠AOG=20°. ∵△BCD为等腰直角三角形,
∴∠CBD=45°. ∴∠HOG=90°. ∴∠AOH=∠AOG+∠GOH=20°+90°=110°.
(2)、如图2所示:连接OG、OE.
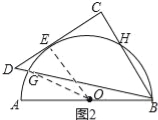
∵DC为圆O的切线,E为切点, ∴∠OED=90°. ∴∠OED=∠C. ∴EO∥CB.
∴∠EOA=∠CBA=β. 又∵∠GBA=![]() ∠GOA=
∠GOA=![]() α,∠ABC=∠ABG+∠DBC, ∴β=
α,∠ABC=∠ABG+∠DBC, ∴β=![]() α+45°.
α+45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家体育馆“鸟巢”的建筑面积达25.8万平方米,请将“25.8万”用科学记数法表示,结果是( )
A.25.8×104
B.25.8×105
C.2.58×104
D.2.58×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于实数a,符号[a]表示不大于a的最大整数,例如:[4.7]=4,[﹣π]=﹣4,[3]=3,如果[
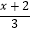 +1]=﹣5,则x的取值范围为 .
+1]=﹣5,则x的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店为调动营业员的积极性,决定实行目标管理,根据每月销售目标完成情况发放奖金.该店统计了每位营业员前半年的月均销售额,并算出所得数据的平均数、众数、中位数,分别为22,15,18(单位:万元).若想让一半左右的营业员都能达到月销售目标,则月销售额定为_____万元较为合适.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从十二边形的一个顶点出发可引_________条对角线,把十二边形分成_______个三角形.
A. 9 10 B. 10 11 C. 11 12 D. 12 13
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x≠0时,下列运算不正确的是( )
A.a2a=a3
B.(﹣a3)2=a6
C.(3a2)2=9a4
D.a3÷a3=a -
科目: 来源: 题型:
查看答案和解析>>【题目】任何一个凸多边形的外角和等于____.它与该多边形的__无关.
相关试题

