【题目】用n边形的对角线把n边形分割成(n-2)个三角形,共有多少种不同的分割方案(n≥4)?
(探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有Pn种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?
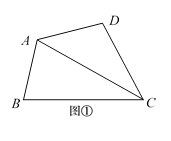
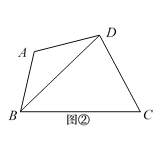
如图①,图②,显然,只有2种不同的分割方案.所以,P4=2.
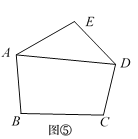
探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?
不妨把分割方案分成三类:
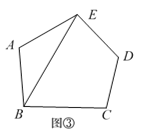
第1类:如图③,用A,E与B连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
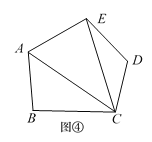
第2类:如图④,用A,E与C连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为![]() 种分割方案.
种分割方案.
第3类:图⑤,用A,E与D连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
所以,P5 =![]() +
+![]() +
+![]() =
=![]() (种)
(种)
探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?
不妨把分割方案分成四类:
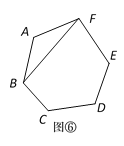
第1类:如图⑥,用A,F与B连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种不同的分割方案.
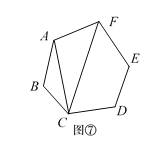
第2类:如图⑦,用A,F与C连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案
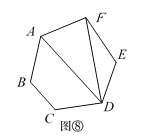
第3类:如图⑧,用A,F与D连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.
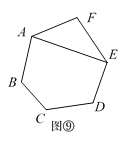
第4类:如图⑨,用A,F与E连接,先把六边形分割转化成1个三角形和1个五边形.再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.
所以,P6 =![]() (种)
(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则P7与P6的关系为:
P7 = ![]() ,共有_____种不同的分割方案.……
,共有_____种不同的分割方案.……
(结论)用n边形的对角线把n边形分割成(
(应用)用八边形的对角线把八边形分割成6个三角形,共有多少种不同的分割方案? (应用上述结论,写出解答过程)
参考答案:
【答案】18;42;![]() ;132种;
;132种;
【解析】
根据题意找到P4,P5,P6之间的关系,进行猜想,然后验证,写出答案.
P4=2,P5 =![]() ,P6=
,P6=![]() ,根据规律可得P7 =
,根据规律可得P7 =![]() =
=![]() =42,进一步推导规律:
=42,进一步推导规律: ![]() ,根据公式,P8=
,根据公式,P8=![]() =132.
=132.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线l:y=﹣x+2与y轴交于点A,抛物线y=(x﹣1)2+k经过点A,其顶点为B,另一抛物线y=(x﹣h)2+2﹣h(h>1)的顶点为D,两抛物线相交于点C.

(1)求点B的坐标,并说明点D在直线l上的理由;
(2)设交点C的横坐标为m.
交点C的纵坐标可以表示为:或;
(3)如图2,若∠ACD=90°,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.

(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图在Rt△ABC中,∠C=90°,tanA= ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)(本小题为选做题)
依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,l1和l2分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
(1)在刚出发时,我公安快艇距走私船多少海里?
(2)计算走私船与公安艇的速度分别是多少?
(3)求出l1,l2的解析式.
(4)问6分钟时,走私船与我公安快艇相距多少海里?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为 m.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=4,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则
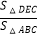 的最大值为 .
的最大值为 . 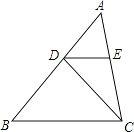
-
科目: 来源: 题型:
查看答案和解析>>【题目】教师运动会中,甲,乙两组教师参加“两人背夹球”往返跑比赛,即:每组两名教师用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.若距起点的距离用y(米)表示,时间用x(秒)表示.下图表示两组教师比赛过程中y与x的函数关系的图象.根据图象,有以下四个推断:
①乙组教师获胜
②乙组教师往返用时相差2秒
③甲组教师去时速度为0.5米/秒
④返回时甲组教师与乙组教师的速度比是2:3
其中合理的是( )
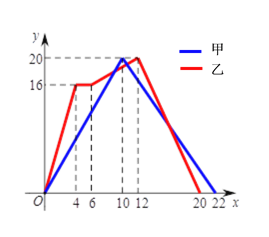
A. ①② B. ①③ C. ②④ D. ①④
相关试题

