Question

【题目】阅读下列文字：
我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如由图1可以得到（a+2b）（a+b）=a2+3ab+2b2 ．
请解答下列问题：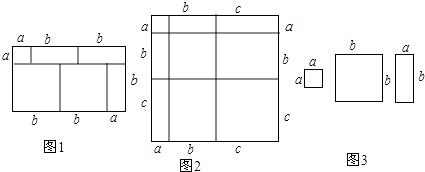

（1）写出图2中所表示的数学等式；
（2）利用（1）中所得到的结论，解决下面的问题：已知a+b+c=12，ab+bc+ac=42，求a2+b2+c2的值；
（3）图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片，请利用所给的纸片拼出一个几何图形，使得用两种不同的方法计算它的面积时，能够得到数学公式：2a2+7ab+3b2=（a+3b）（2a+b）．

Answer 1

【答案】
（1）

解：正方形的面积可表示为=（a+b+c）2；

正方形的面积=各个矩形的面积之和=a2+b2+c2+2ab+2bc+2ca，

所以（a+b+c）2=a2+b2+c2+2ab+2bc+2ca

（2）

解：∵a+b+c=12，ab+bc+ac=42，

∴由（1）可知：a2+b2+c2=（a+b+c）2﹣2（ab+bc+ca）=122﹣42×2=60

（3）

解：如图所示：

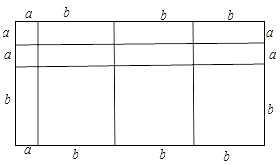
2a2+7ab+3b2=（a+3b）（2a+b）

【解析】（1）直接求得正方形的面积，然后再根据正方形的面积=各矩形的面积之和求解即可；（2）将a+b+c=12，ab+bc+ac=42代入（1）中得到的关系式，然后进行计算即可；（3）根据分解结果画出图形即可．