【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F. 
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD; 
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD. 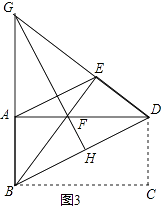
参考答案:
【答案】
(1)证明:∵△BCD≌△BED,
∴∠DBC=∠EBD,
又∵四边形ABCD是长方形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠EBD,
∴BF=DF
(2)证明:∵四边形ABCD是长方形,
∴AD=BC=BE,
又∵FB=FD,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF+∠AFE=2∠FBD+∠BFD=180°,
∴∠AEF=∠FBD,
∴AE∥BD
(3)证明:∵四边形ABCD是长方形,
∴AD=BC=BE,AB=CD=DE,BD=DB,
在△ABD与△EDB中,
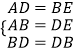
∴△ABD≌△EDB(SSS),
∴∠ABD=∠EDB,
∴GB=GD,
又∵FB=FD,
∴GF是BD的垂直平分线,即GH垂直平分BD
【解析】(1)由折叠的性质可得到△ABD≌△EDB,那么∠ADB=∠EBD,所以BF=DF;(2)根据长方形的性质可得和三角形内角和定理可得∠AEF=∠FBD,再根据平行线的判定即可求解;(3)先SSS证明△ABD≌△EDB,再根据全等三角形的性质和垂直平分线的性质即可求解.
【考点精析】本题主要考查了翻折变换(折叠问题)的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2a2+[a2+(3a2-2a)-2(a2-3a)] 其中a=-
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司员工上班方式的条形统计图如图所示:
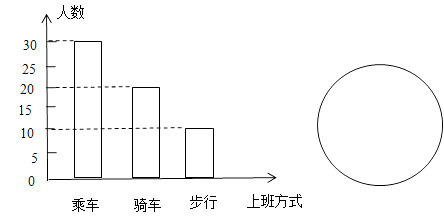
(1)这个公司共有多少名员工?
(2)根据条形统计图,制作相应的扇形统计图. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是关于x的方程2x+3a﹣1=0的解,则a的值是( )
A.﹣1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,
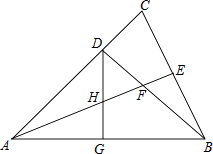
(1)求∠ACB的度数;
(2)HE= AF.
AF. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a3(3an-2am+4ak)=3a9-2a6+4a4,则m,n,k的值分别为( )
A. 6,3,1 B. 3,6,1 C. 2,1,3 D. 2,3,1
-
科目: 来源: 题型:
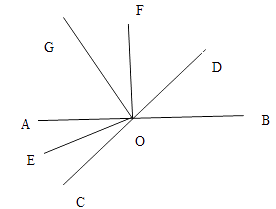
查看答案和解析>>【题目】如图,AB与CD相交于O , OE平分∠AOC , OF⊥AB于O , OG⊥OE于O , 若∠BOD=40°,求∠AOE和∠FOG的度数.
相关试题

