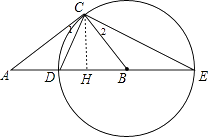
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
参考答案:
【答案】
(1)证明:∵DE为直径,
∴∠DCE=90°,即∠2+∠DCB=90°,
∵∠ACB=90°,即∠1+∠DCB=90°,
∴∠1=∠2,
而∠CAD=∠EAC,
∴△ACD∽△AEC
(2)解:由 ![]() =
= ![]() ,设AC=4k,则BC=3k,
,设AC=4k,则BC=3k,
∴BD=BE=3k,
∴AB= ![]() =5k,
=5k,
∴AE=AB+BE=5k+3k=8k,
在Rt△CDE中,tanE= ![]() ,
,
∵△ACD∽△AEC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴tanE= ![]()
(3)作CH⊥AE于H,如图,
∵△ACD∽△AEC,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,解得AE=12,CE=
,解得AE=12,CE= ![]() CD,
CD,
∴DE=AE﹣AC=8,
在Rt△CDE中,∵tanE= ![]() =
= ![]() =
= ![]() ,
,
∴∠E=30°,
∴CD= ![]() DE=4,CE=4
DE=4,CE=4 ![]() ,
,
在Rt△CHE中,CH= ![]() CE=2
CE=2 ![]() ,
,
∴△ACE的面积= ![]() ×12×2
×12×2 ![]() =12
=12 ![]() .
.
【解析】(1)利用圆周角定理得到∠DCE=90°,而∠ACB=90°,则∠1=∠2,加上公共角,则可判断△ACD∽△AEC;(2)利用由 ![]() =
= ![]() 设AC=4k,BC=3k,由勾股定理计算出AB=5k,则AE=8k,再由△ACD∽△AEC,利用相似比得到
设AC=4k,BC=3k,由勾股定理计算出AB=5k,则AE=8k,再由△ACD∽△AEC,利用相似比得到 ![]() =
= ![]() =
= ![]() ,然后根据正切的定义可得tanE的值;(3)作CH⊥AE于H,如图,由△ACD∽△AEC,利用相似比得到AE=12,CE=
,然后根据正切的定义可得tanE的值;(3)作CH⊥AE于H,如图,由△ACD∽△AEC,利用相似比得到AE=12,CE= ![]() CD,则DE=AE﹣AC=8,在Rt△CDE中利用三角函数和特殊角的三角形函数值得到∠E=30°,则可计算出CD=
CD,则DE=AE﹣AC=8,在Rt△CDE中利用三角函数和特殊角的三角形函数值得到∠E=30°,则可计算出CD= ![]() DE=4,CE=4
DE=4,CE=4 ![]() ,接着计算出CH,然后根据三角形面积公式求解.
,接着计算出CH,然后根据三角形面积公式求解.
-
科目: 来源: 题型:
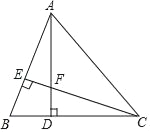
查看答案和解析>>【题目】如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且
 .
. 
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】京东商城销售A、B两种型号的电风扇,销售单价分别为250元、180元,如表是近两周的销售利润情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)

(1)求A、B两种型号电风扇的每台进价;
(2)若京东商城准备用不多于5万元的金额采购这两种型号的电风扇共300台,求A种型号的电风扇最多能采购多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;(图1)
(2)求∠FAE的度数;(图1)
(3)如图2,延长CF到G点,使BF=GF,连接AG.求证:CD=CG;并猜想CD与2BF+DE的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(﹣1,0),C(0,﹣5)两点,与x轴交于点B.

(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q?若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
相关试题

