【题目】已知抛物线y=﹣x2+![]() x+2与直线y=
x+2与直线y=![]() x+2相交于点C和D,点P是抛物线在第一象限内的点,它的横坐标为m,过点P作PE⊥x轴,交CD于点F.
x+2相交于点C和D,点P是抛物线在第一象限内的点,它的横坐标为m,过点P作PE⊥x轴,交CD于点F.
(1)求点C和D的坐标;
(2)求抛物线与x轴的交点坐标;
(3)如果以P、C、O、F为顶点的四边形是平行四边形,求m的值.

参考答案:
【答案】(1)C(0,2)和D(3,![]() );(2)(
);(2)(![]() ,0),(4,0);(3)m的值为1、2或
,0),(4,0);(3)m的值为1、2或![]() .
.
【解析】
(1)解抛物线和直线的解析式组成的方程组即可;
(2)令y=0,解一元二次方程即可;
(3)若四边形PCOF是平行四边形,则PF=OC=2,先化简题意表示出点P的坐标为(m,-m2+![]() m+2),点F的坐标为(m,
m+2),点F的坐标为(m,![]() m+2),然后分两种情况讨论求得;
m+2),然后分两种情况讨论求得;
(1)解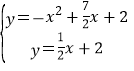 ,则x2+
,则x2+![]() x+2=
x+2=![]() x+2,
x+2,
整理得,x2-3x=0,解得x1=0,x2=3,
∴![]() ,
,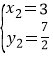 .
.
∴所求的点的坐标是C(0,2)和D(3,![]() );
);
(2)令y=0,则x2+![]() x+2=0,
x+2=0,
解得,x1=![]() ,x2=4,
,x2=4,
∴抛物线与x轴的交点坐标为(![]() ,0),(4,0);
,0),(4,0);
(3)若四边形PCOF是平行四边形,则PF=OC=2,
∵点P的横坐标为m,
∴点P的坐标为(m,-m2+![]() m+2),点F的坐标为(m,
m+2),点F的坐标为(m,![]() m+2),
m+2),
当0<m<3时,PF=(-m2+![]() m+2)-(
m+2)-(![]() m+2),
m+2),
∴-m2+3m=2,m2-3m+2=0,m1=1,m2=2;
当3<m<4时,PF=(![]() m+2)-(-m2+
m+2)-(-m2+![]() m+2),
m+2),
∴m2-3m=2,m2-3m-2=0,m3=![]() ,m4=
,m4=![]() (舍去).
(舍去).
∴如果以P、C、O、F为顶点的四边形是平行四边形,则m的值为1、2或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店老板用400元购进一批葡萄,由于葡萄新鲜很快售完,老板又用500元购进第二批葡萄,所购数量与第一批相同,但每千克进价比第一批贵2元.
(1)求第一批葡萄进价为每千克多少元;
(2)若老板以每千克11元的价格将两批葡萄全部售完,可以盈利多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

(1)在方格纸中作出与△ABC关于原点对称的△A1B1C1,并写出点A
 、B
、B 、C
、C 的坐标;
的坐标;(2)求出过A
 、B
、B 、O三点的抛物线的对称轴.
、O三点的抛物线的对称轴. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2﹣2x+3用配方法化成y=a(x﹣h)2+k的形式是________,抛物线与x轴的交点坐标是________,抛物线与y轴的交点坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米.如果梯子的顶端沿墙面下滑0.4米,那么点B将向左滑动多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小王于上午8时从甲地出发去相距50千米的乙地. 右图中,折线
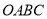 是表示小王离开甲地的时间
是表示小王离开甲地的时间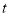 (时)与路程
(时)与路程 (千米)之间的函数关系的图像.根据图像给出的信息,下列判断中,错误的是( )
(千米)之间的函数关系的图像.根据图像给出的信息,下列判断中,错误的是( )
A.小王11时到达乙地
B.小王在途中停了半小时
C.与8:009:30相比,小王在10:0011:00前进的速度较慢
D.出发后1小时,小王走的路程少于25千米
相关试题

