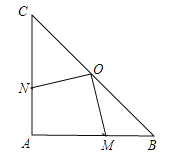
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM .
(1)证明:OM = ON;
(2)四边形AMON面积是否发生变化,若发生变化说明理由;若不变,请你求出四边形AMON的面积.
参考答案:
【答案】(1)见解析 (2)4cm2
【解析】试题分析:
(1) 分析条件可知,要证明OM=ON需要利用全等三角形进行. 易知△ABC是等腰直角三角形,根据“O是BC的中点”这一条件容易联想到利用等腰三角形“三线合一”的性质来构造全等三角形. 连接OA后容易发现△OAN与△OBM全等,进而得到OM=ON.
(2) 借助第(1)小题的辅助线作法可知,AO将四边形AMON分割为△OAN与△OAM. 由第(1)小题的证明可知,△OAN的面积等于△OBM的面积. 利用这一关系,实际上将四边形AMON的面积转化为了△OAB的面积. 因为△OAB的面积不受动点运动的影响,所以四边形AMON的面积不变. 根据等腰三角形的性质容易求得△OAB的面积,即得四边形AMON的面积.
试题解析:
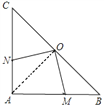
(1) 连接OA. (如图)
∵在Rt△ABC中,AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,即∠ABO=45°,
∵O是BC的中点,且△ABC是等腰直角三角形,
∴AO⊥BC,
∴在Rt△AOB中,∠OAB=90°-∠ABO=90°-45°=45°,
∴∠OAB=∠ABO,
∴OA=OB,
∵O是BC的中点,且△ABC是等腰直角三角形,
又∵∠BAC=90°,
∴![]() ,
,
∴∠OAC=∠ABO=45°,即∠OAN=∠OBM,
∵在△OAN与△OBM中:
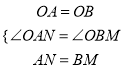 ,
,
∴△OAN≌△OBM (SAS),
∴ON=OM,即OM=ON.
(2) 在动点运动过程中,四边形AMON面积不变.
下面求解四边形AMON的面积.
连接OA.
由第(1)小题的证明可知:△OAN≌△OBM,
∴△OAN的面积等于△OBM的面积,
∵四边形AMON的面积等于△OAN的面积与△OAM的面积之和,
∴四边形AMON的面积等于△OBM的面积与△OAM的面积之和,
∵△OBM的面积与△OAM的面积之和等于△OAB的面积,
∴四边形AMON的面积等于△OAB的面积,
∵O是BC的中点,且△ABC是等腰直角三角形,
∴△OAB的面积等于△ABC的面积的一半,
∵AB=AC=4cm,
∴Rt△ABC的面积为: ![]() (cm2),
(cm2),
∴△OAB的面积为: ![]() (cm2),
(cm2),
∴四边形AMON的面积为:4cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

-
科目: 来源: 题型:
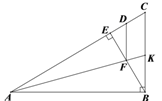
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;
(2)求证:FD∥BC .
-
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图

① ∵

∴ ______// _____(______________________)
② ∵∠DAB+∠ABC=180°
∴ _____// _____(__________________)
③∵ AB // CD
∴∠_____+∠ABC=180°(___________________)
④∵ ______// ______
∴∠C=∠3(_______________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”,是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化,某校为各班购进《三国演义》和《水浒传》连环画若干套,其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元,用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍,求每套《水浒传》连环画的价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料
小明遇到这样一个问题:求计算
 所得多项式的一次项系数.
所得多项式的一次项系数.小明想通过计算
 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.他决定从简单情况开始,先找
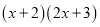 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现: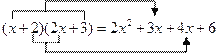
也就是说,只需用
 中的一次项系数1乘以
中的一次项系数1乘以 中的常数项3,再用
中的常数项3,再用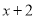 中的常数项2乘以
中的常数项2乘以 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加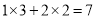 ,即可得到一次项系数.
,即可得到一次项系数.延续上面的方法,求计算
 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用 的一次项系数1,
的一次项系数1,  的常数项3,
的常数项3, 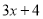 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用 的一次项系数2,
的一次项系数2,  的常数项2,
的常数项2,  的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用 的一次项系数3,
的一次项系数3,  的常数项2,
的常数项2,  的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.参考小明思考问题的方法,解决下列问题:
(1)计算
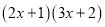 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .(2)计算
 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .(3)若计算
 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则 =_________.
=_________.(4)若
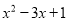 是
是 的一个因式,则
的一个因式,则 的值为 .
的值为 .
相关试题

