Question

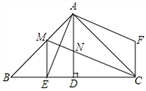
【题目】如图，中，垂足是D，AE平分，交BC于点E，在外有一点F，使.

（1）求∠ACF的度数；

（2）求证：；

（3）在AB上取一点M，使，连接MC，交AD于点N，连接ME.求证：.

Answer 1

【答案】（1）45°；（2）证明见解析；（3）证明见解析.

【解析】试题分析：（1）根据等腰直角三角形的性质求出∠B=∠ACB=45°，再求出∠ACF=45°；

（2）由∠B =45°，∠ACF=45°，得到∠B=∠ACF，根据同角的余角相等求出∠BAE=∠CAF，然后利用“角边角”证明△ABE和△ACF全等，根据全等三角形对应边相等证明即可；

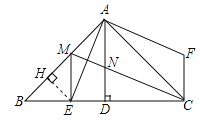
（3）过点E作EH⊥AB于H，求出△BEH是等腰直角三角形，然后求出HE=BH，再根据角平分线上的点到角的两边距离相等可得DE=HE，然后求出HE=HM，从而得到△HEM是等腰直角三角形，再根据等腰直角三角形的性质求解即可．

试题解析：（1）∵∠BAC=90°，AB=AC，∴∠B=∠ACB=45°，∵FC⊥BC，∴∠BCF=90°，∴∠ACF=90°﹣45°=45°；

（2）∵∠B =45°，∠ACF=45°，∴∠B=∠ACF．

∵∠BAC=90°，FA⊥AE，∴∠BAE+∠CAE=90°，∠CAF+∠CAE=90°，∴∠BAE=∠CAF．

在△ABE和△ACF中，∵∠BAE＝∠CAF，AB＝AC，∠B＝∠ACF

∴△ABE≌△ACF（ASA），∴BE=CF；

（3）如图，过点E作EH⊥AB于H，则△BEH是等腰直角三角形，∴HE=BH，∠BEH=45°．

∵AE平分∠BAD，AD⊥BC，∴DE=HE，∴DE=BH=HE．

∵BM=2DE，∴HE=HM，∴△HEM是等腰直角三角形，∴∠MEH=45°，∴∠BEM=45°+45°=90°，∴ME⊥BC．