【题目】在ΔABC中点D为BC上一点,E为AC上一点,连接AD、BE、DE,已知BD=DE,AD=DC,∠ADB=∠CDE.
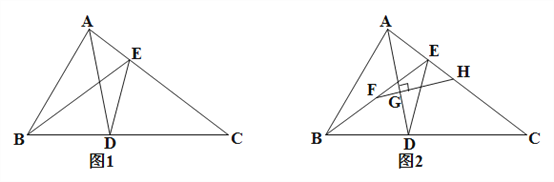
(1)如图1,若∠ACB=40°时,求∠BAC的度数.
(2)如图2,F是BE的中点,过点F作AD的垂线,分别交AD、AC于点G、H,求证:AH=CH.
参考答案:
【答案】(1)80°;(2)证明见解析
【解析】试题分析:(1)易证ΔADB≌ΔCDE,得∠ACB=∠DAC=∠DAB=40°,故∠BAC=80°;
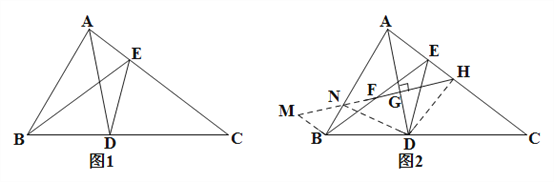
(2)延长HF至点M使FM=FH,交AB于点N,连接BM、DH、DN,得ΔBMF≌ΔEHF,得BM=EH,∠EHF=∠M,结合(1)的结论可证明ΔAGN≌ΔAGH得BM=BN=EH,利用线段垂直平分线的性质得DN=DH ∠ADN=∠ADH,从而可证ΔBDN≌ΔEDH,继而证出∠ADH=∠CDH,进一步得出:AH=CH
试题解析:
简要过程:
(1)∵ΔADB≌ΔCDE (SAS)
∴∠ACB=∠DAC=∠DAB=40°
∴∠BAC=80°
(2)延长HF至点M使FM=FH,交AB于点N,连接BM、DH、DN
∴ΔBMF≌ΔEHF
∴BM=EH,∠EHF=∠M
由①得∠DAC=∠DAB,且FH⊥AD
∴ΔAGN≌ΔAGH
∴∠ANG=∠AHG
∵∠ANG=∠BNM
∴∠M=∠BNM
∴BM=BN=EH
∵ΔADN≌ΔADH(或用中垂线的性质)
∴DN=DH ∠ADN=∠ADH
∴ΔBDN≌ΔEDH(SSS)
∴∠BDN=∠EDH
∴∠ADB-∠BDN=∠CDE-∠EDH
∴∠ADN=∠CDH
∴∠ADH=∠CDH
∴AH=CH
-
科目: 来源: 题型:
查看答案和解析>>【题目】2-1的倒数是( )
A.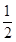
B.-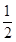
C.2
D.-2 -
科目: 来源: 题型:
查看答案和解析>>【题目】若(x2011)0+(
 )2有意义,则x的取值范围是( )
)2有意义,则x的取值范围是( )
A.x≠2011
B.x≠2011且x≠2012
C.x≠2011且x≠2012且x≠0
D.x≠2011且x≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣2(x﹣6)2+8的顶点坐标是( )
A.(6,8)B.(﹣6,﹣8)C.(﹣6,8)D.(6,﹣8)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度是________ m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2mx+m2+3(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?
(3)将抛物线y=x2﹣2mx+m2+3(m是常数)图象在对称轴左侧部分沿直线y=3翻折得到新图象为G,若与直线y=x+2有三个交点,请直接写出m的取值范围.
相关试题

