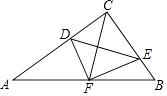
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为 . 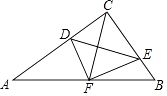
参考答案:
【答案】![]()
【解析】解:由折叠可得,∠DCE=∠DFE=90°, ∴D,C,E,F四点共圆,
∴∠CDE=∠CFE=∠B,
又∵CE=FE,
∴∠CFE=∠FCE,
∴∠B=∠FCE,
∴CF=BF,
同理可得,CF=AF,
∴AF=BF,即F是AB的中点,
∴Rt△ABC中,CF= ![]() AB=5,
AB=5,
由D,C,E,F四点共圆,可得∠DFC=∠DEC,
由∠CDE=∠B,可得∠DEC=∠A,
∴∠DFC=∠A,
又∵∠DCF=∠FCA,
∴△CDF∽△CFA,
∴CF2=CD×CA,即52=CD×8,
∴CD= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了勾股定理的概念和翻折变换(折叠问题)的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于 .

-
科目: 来源: 题型:
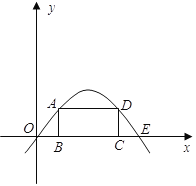
查看答案和解析>>【题目】如图:矩形ABCD的顶点B、C在x轴的正半轴上,A、D在抛物线
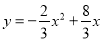 上,矩形的顶点均为动点,且矩形在抛物线与
上,矩形的顶点均为动点,且矩形在抛物线与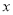 轴围成的区域里。
轴围成的区域里。(1)设A点的坐标为(
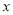 ,
,  ),试求矩形周长
),试求矩形周长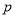 关于变量
关于变量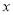 的函数表达式;
的函数表达式;(2)是否存在这样的矩形,它的周长为9,试证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的周长为16,面积为8
 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 . 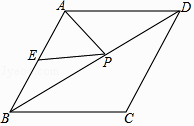
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.3a+2b=5ab
B.2a3+3a2=5a5
C.3a2b﹣3ba2=0
D.5a2﹣4a2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x-8<0的正整数解有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3﹣(﹣1)= .
相关试题

